こんにちは、JS2IIUです。
これまで、「1次元カルマン・フィルタ」で基礎を固め、「2次元カルマン・フィルタ」で行列演算を用いたマルチトラッキングを体験してきました。ここまでは順調でしたね。しかし、私たちが生きているこの現実世界には、ある残酷な事実があります。
それは、「世界は直線でできていない」ということです。
前回のモデルでは「等速直線運動」を仮定しましたが、現実の車はハンドルを切ればカーブします。ドローンは複雑に姿勢を変えます。ロボットアームは円弧を描いて動きます。これらはいずれも、入力と出力が比例関係にない「非線形システム (Non-linear System)」です。
線形(直線)を前提とした標準的なカルマン・フィルタに、カーブ全開のデータを入力するとどうなるでしょうか?予測は破綻し、推定値はあさっての方向へ飛んでいきます。
そこで登場するのが、実務レベルのロボット制御や自動運転でデファクトスタンダードとして君臨する「拡張カルマン・フィルタ(Extended Kalman Filter: EKF)」です。
この記事では、EKFがどのようにして非線形な現象を扱っているのか、その数学的なトリックである「線形化」と「ヤコビ行列」の正体を暴き、Pythonコードで実際にカーブするロボットを追跡してみます。今回もよろしくお願いします
1. 概念編
なぜ標準カルマン・フィルタではダメなのか?
標準のカルマン・フィルタは、以下の式(状態空間モデル)が成り立つことを前提としています。
$$
\mathbf{x}_{t+1} = F \mathbf{x}_t + B \mathbf{u}_t
$$
ここで \( F \) は定数の行列です。これは「次の状態は、今の状態の定数倍(線形結合)になる」と言っています。
しかし、例えば車がハンドルを角度 \( \theta \) だけ切って速度 \( v \) で進む場合、位置の変化は以下のように三角関数を含んだ形になります。
$$
x_{t+1} = x_t + v \cos(\theta) \Delta t \
y_{t+1} = y_t + v \sin(\theta) \Delta t
$$
\( \cos \) や \( \sin \) は非線形関数です。これを無理やり (F\mathbf{x}) という行列の掛け算だけで表現することは不可能です。ここで標準カルマン・フィルタは無力化されます。
解決策:曲がっているなら、ズームすればいい
この問題に対するEKFの解決策は非常にシンプルで、かつ強力です。
「どんなに曲がっている曲線でも、顕微鏡で拡大して見れば、その一瞬だけは直線に見えるはずだ」
これが線形化 (Linearization) の考え方です。
数学的には、ある一点における接線を引くことに相当します。これをテーラー展開 (Taylor Series Expansion) の1次近似と呼びます。
EKFは、予測を行うたびに「今のこの場所において、カーブはどの方向へ向かっているか(接線の傾き)」を計算し、「その一瞬だけ有効な行列 \(F\) 」 を動的に作り出します。この「動的な傾き行列」こそが、今回の主役であるヤコビ行列 (Jacobian Matrix) です。
「ヤコビ行列」の正体
「ヤコビ行列」と聞くと身構えてしまうかもしれませんが、恐れる必要はありません。
1変数の関数 \( y = f(x) \) の傾きは、微分 \( \frac{dy}{dx} \) で求められました。
ヤコビ行列は、これを多変数(ベクトル)に拡張しただけのものです。
入力が複数( \( x, y, \theta \) )、出力も複数(次の \( x, y, \theta \) )あるシステムにおいて、「\( x \) がちょっと変わったら出力はどう変わる?」「 \( \theta \) がちょっと変わったら?」という「変化率の総当たり表」。それがヤコビ行列です。
2. 実装準備:ロボットの動きをモデル化する
今回は、ロボット工学で最も一般的な「対向2輪モデル(差動二輪)」を扱います。ルンバのような、左右のタイヤの速度差で旋回するロボットをイメージしてください。
状態ベクトルと制御入力
ロボットの状態 \( \mathbf{x} \) と、ロボットへの指令(制御入力)\( \mathbf{u} \) を以下のように定義します。
- 状態 \( \mathbf{x} \): \([x, y, \theta]^T \) (位置X, 位置Y, 向いている角度)
- 入力 \( \mathbf{u} \): \([v, \omega]^T \) (並進速度, 回頭角速度)
状態方程式(非線形モデル)
時間 \( \Delta t \) 後の状態を計算する関数 \( f(\mathbf{x}, \mathbf{u}) \) は以下のようになります。
$$
\begin{bmatrix} x’ \\ y’ \\ \theta’ \end{bmatrix} =
\begin{bmatrix} x \\ y \\ \theta \end{bmatrix} +
\begin{bmatrix} v \cos(\theta) \Delta t \\ v \sin(\theta) \Delta t \\ \omega \Delta t \end{bmatrix}
$$
これをPythonコードで書くとこうなります。
import numpy as np
def motion_model(x, u, dt):
"""
非線形な移動モデル
x: 状態ベクトル [x, y, theta]
u: 制御入力 [v, omega]
"""
theta = x[2]
v = u[0]
omega = u[1]
# 状態遷移 (非線形)
x_next = x[0] + v * np.cos(theta) * dt
y_next = x[1] + v * np.sin(theta) * dt
theta_next = theta + omega * dt
return np.array([x_next, y_next, theta_next])ヤコビ行列の導出
さて、ここでEKFのためにヤコビ行列 \( J_F \) を計算する必要があります。
上記の式を、状態変数 \( x, y, \theta \) でそれぞれ偏微分 (Partial Differentiation) します。
$$
J_F = \frac{\partial f}{\partial \mathbf{x}} =
\begin{bmatrix}
\frac{\partial x’}{\partial x} & \frac{\partial x’}{\partial y} & \frac{\partial x’}{\partial \theta} \\
\frac{\partial y’}{\partial x} & \frac{\partial y’}{\partial y} & \frac{\partial y’}{\partial \theta} \\
\frac{\partial \theta’}{\partial x} & \frac{\partial \theta’}{\partial y} & \frac{\partial \theta’}{\partial \theta}
\end{bmatrix}=
\begin{bmatrix}
1 & 0 & -v \sin(\theta) \Delta t \\
0 & 1 & v \cos(\theta) \Delta t \\
0 & 0 & 1
\end{bmatrix}
$$
この行列が、「現在の角度 \( \theta \) と速度 \( v \) における、次の瞬間の変化の傾向」を表しています。これをコードに落とし込みます。
def jacobian_f(x, u, dt):
"""
状態遷移関数のヤコビ行列を計算
"""
theta = x[2]
v = u[0]
# 上記の数式をそのままコードにする
# 3x3 行列
J = np.array([
[1.0, 0.0, -v * np.sin(theta) * dt],
[0.0, 1.0, v * np.cos(theta) * dt],
[0.0, 0.0, 1.0]
])
return Jコラム:数式が苦手なあなたへ(自動微分の活用)
「偏微分なんて手計算したくない!」という方もいるでしょう。現代のAI開発では、PyTorchやJAX、SymPyといったライブラリを使えば、関数を定義するだけで自動的にヤコビ行列を計算してくれます(自動微分)。今回は基本を理解するためにNumPyで書き下しますが、実務ではそれらを使うのが賢い選択です。
3. 実践編:PythonによるEKFの実装
それでは、EKFのクラスを作成します。
標準KFとの最大の違いは、predictメソッド内で「単純な行列の掛け算」ではなく「非線形関数の実行」と「ヤコビ行列の計算」を行う点です。
class ExtendedKalmanFilter:
def __init__(self, dt, initial_state, initial_cov, process_noise, measurement_noise):
self.dt = dt
self.x = initial_state # [x, y, theta]
self.P = initial_cov # 共分散行列
self.Q = process_noise # プロセスノイズ Q
self.R = measurement_noise # 観測ノイズ R
def predict(self, u):
"""
予測ステップ (Time Update)
"""
# 1. 非線形関数による状態予測
# x = f(x, u)
self.x = motion_model(self.x, u, self.dt)
# 2. ヤコビ行列 F の計算
F = jacobian_f(self.x, u, self.dt)
# 3. 誤差共分散の予測
# P = FPF^T + Q (Fはヤコビ行列)
self.P = F @ self.P @ F.T + self.Q
def update(self, z):
"""
更新ステップ (Measurement Update)
ここでは観測モデルは線形と仮定 (GPSで直接 x, y を測れる)
もし観測も非線形(レーダーの距離と角度など)なら、ここでもヤコビ行列 H が必要。
"""
# 観測行列 H (3次元の状態から x, y だけを取り出す)
H = np.array([
[1, 0, 0],
[0, 1, 0]
])
# 観測残差
y = z - H @ self.x
# --- 以下は標準KFと同じ ---
S = H @ self.P @ H.T + self.R
K = self.P @ H.T @ np.linalg.inv(S)
# 推定値の更新
self.x = self.x + K @ y
# 共分散の更新
I = np.eye(len(self.x))
self.P = (I - K @ H) @ self.P比較実験:8の字走行
EKFの威力を確認するため、ロボットに「8の字」を描くような複雑な動きをさせてみましょう。
比較対象として、オドメトリ(制御入力の積み上げ)のみの場合と、EKFで観測値を取り入れた場合を表示します。
import matplotlib.pyplot as plt
# --- シミュレーション設定 ---
dt = 0.1
steps = 1000
# 真の状態・推定値の保存用
true_states = []
dead_reckoning = [] # 推測航法(補正なし)
ekf_estimates = []
measurements = []
# 初期状態
state_true = np.array([0.0, 0.0, 0.0])
state_dr = np.array([0.0, 0.0, 0.0]) # Dead Reckoning用
# EKF初期化
Q = np.diag([0.1, 0.1, np.deg2rad(1.0)]) ** 2 # プロセスノイズ
R = np.diag([1.0, 1.0]) ** 2 # 観測ノイズ (GPS精度)
ekf = ExtendedKalmanFilter(dt, np.zeros(3), np.eye(3), Q, R)
# --- ループ実行 ---
for i in range(steps):
t = i * dt
# 制御入力生成 (8の字を描くように角速度を変化させる)
v = 1.0 # 一定速度
omega = 0.2 * np.sin(t / 10.0) # 角速度を正弦波で揺らす
u = np.array([v, omega])
# 1. 真の状態を更新 (ノイズなし)
state_true = motion_model(state_true, u, dt)
true_states.append(state_true)
# 2. 推測航法 (Dead Reckoning) - ノイズを含んだ入力のみで計算
# 実際の制御にはノイズが乗る
u_noisy = u + np.random.normal(0, [0.1, 0.05])
state_dr = motion_model(state_dr, u_noisy, dt)
dead_reckoning.append(state_dr)
# 3. 観測データの生成 (GPS) - 真の位置にノイズを乗せる
z = state_true[:2] + np.random.normal(0, 1.0, 2)
measurements.append(z)
# 4. EKFの実行
ekf.predict(u_noisy) # ノイズありの入力で予測
ekf.update(z) # ノイズありの観測で修正
ekf_estimates.append(ekf.x)
# --- NumPy配列へ変換 ---
true_states = np.array(true_states)
dead_reckoning = np.array(dead_reckoning)
ekf_estimates = np.array(ekf_estimates)
measurements = np.array(measurements)
# --- 可視化 ---
plt.figure(figsize=(10, 8))
plt.plot(true_states[:, 0], true_states[:, 1], 'k-', label="Ground Truth", linewidth=2)
plt.plot(dead_reckoning[:, 0], dead_reckoning[:, 1], 'r--', label="Dead Reckoning (No Correction)")
plt.scatter(measurements[:, 0], measurements[:, 1], c='gray', s=5, label="GPS Measurements", alpha=0.5)
plt.plot(ekf_estimates[:, 0], ekf_estimates[:, 1], 'b-', label="EKF Estimate", linewidth=3)
plt.title("EKF Robot Tracking (Figure 8 Path)")
plt.xlabel("X [m]")
plt.ylabel("Y [m]")
plt.legend()
plt.grid(True)
plt.axis("equal")
plt.show()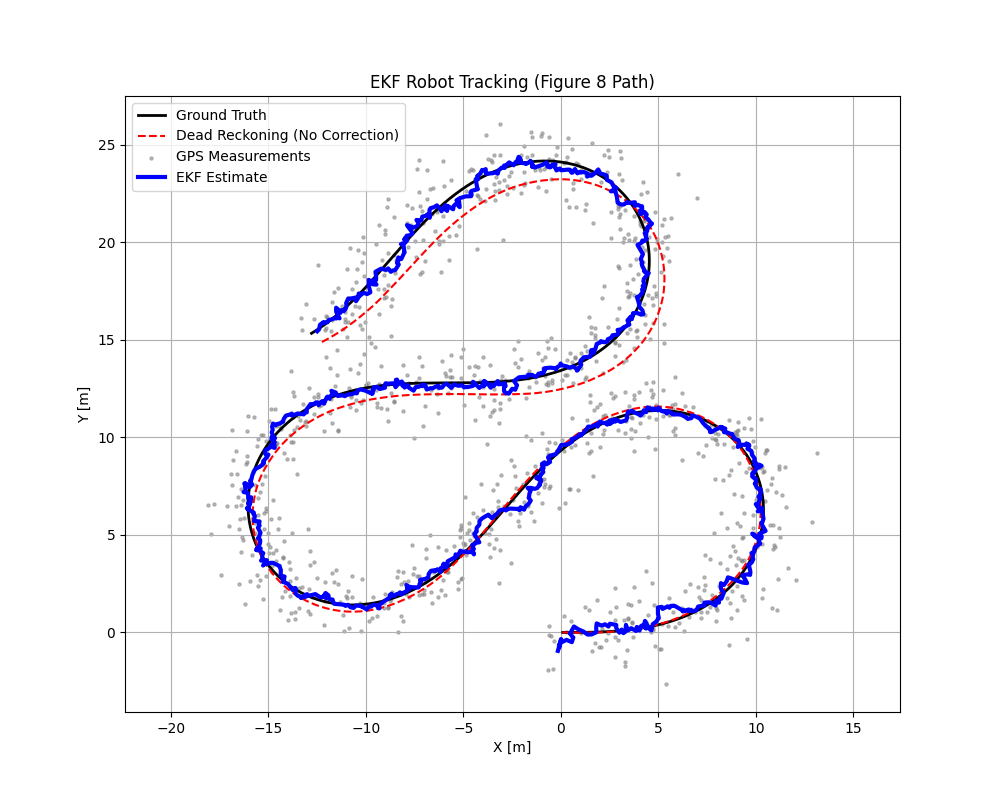
結果の考察
このコードを実行すると、以下の現象が確認できるはずです。
- 黒い線(真の値): きれいな8の字を描いています。
- 赤い点線(補正なし): 制御入力のノイズが累積し、時間とともに真の軌道からどんどん離れていき、形が崩れてしまいます。これがオドメトリ(推測航法)の限界です。
- 灰色の点(観測値): 真の軌道の周りにバラついていますが、全体的な形状は捉えています。
- 青い線(EKF): 赤い線のように発散することなく、かといって灰色の点のようにガタつくこともなく、滑らかに黒い線(真の値)を追従し続けています。
これこそが、非線形モデルとヤコビ行列を用いたEKFの効果です。「曲がる」というモデルの性質を正しく理解しているため、少ない情報から高い精度で位置を推定できるのです。
4. まとめと展望
今回は、カルマン・フィルタを実世界の問題に応用するための「拡張カルマン・フィルタ(EKF)」について解説しました。
今回のポイント
- 非線形システム: 現実世界(ロボットや車)は直線だけでは表現できない。
- 線形化: 「局所的には直線である」という仮定で近似する。
- ヤコビ行列: 多変数の変化率を表す行列。これを毎回計算することで、非線形モデルを扱えるようになる。
さらに高度な技術へ
EKFは強力ですが、弱点もあります。ヤコビ行列の計算が複雑で面倒なことや、近似精度が悪くなると推定が破綻することです。
これらを解決するために、以下のような発展手法が存在します。
- Unscented Kalman Filter (UKF): ヤコビ行列を計算せず、「シグマ点」という代表点を飛ばして分布の変化を近似する手法。実装が楽で精度も高い場合が多いです。
- パーティクル・フィルタ (Particle Filter): ガウス分布すら仮定しない手法。確率の粒(粒子)を大量にばら撒いて推定します。計算量は多いですが、最強の柔軟性を持ちます。
しかし、すべての基礎は今回のEKFにあります。「モデルを作って、近似して、修正する」というエンジニアリングの神髄を、ぜひこのコードから感じ取ってください。
最後まで読んでいただきありがとうございました。



コメント