こんにちは、JS2IIUです。
前回の記事では、1次元のシンプルなデータを対象に、カルマン・フィルタがどのようにノイズを除去し、真の値を推定するかを解説しました。今回はその続編として、舞台を2次元へと移します。
現実世界の問題、例えばドローンの制御、自動運転車のマッピング、あるいはマウスカーソルの追跡などは、単なる数値の増減ではなく、空間上の「位置」や「速度」といった複数の要素が絡み合っています。これらを扱うには、1次元の知識だけでは不十分です。
そこで登場するのが「行列(Matrix)」と「状態ベクトル」です。
「行列計算が出てくると急に難しく感じる」という方もいるかもしれませんが、安心してください。Pythonの強力な数値計算ライブラリであるNumPyを使えば、複雑な計算はすべてライブラリに任せることができます。
この記事では、位置情報(GPSなど)しか得られない状況から、滑らかな位置の追跡を行い、さらに直接は観測できない「速度」までも推定してしまう、カルマン・フィルタの「状態空間モデル」としての真価を、コードを通じて体験していただきます。今回もよろしくお願いします。
1. 理論編:行列で語る「状態」の世界
1次元のときは変数 \(x\) 一つで済みましたが、2次元平面を移動する物体を扱う場合、私たちは以下の4つの情報を同時に管理したくなります。
- X座標 \(p_x\)
- Y座標 \(p_y\)
- X方向の速度 \(v_x\)
- Y方向の速度 \(v_y\)
これらをバラバラに計算するのではなく、一つの縦長のベクトルにまとめて扱うのがカルマン・フィルタの作法です。これを状態ベクトル(State Vector)と呼びます。
状態ベクトルと行列演算
今回のモデルでは、状態ベクトル \( \mathbf{x} \) を以下のように定義します。
\[
\mathbf{x} = \begin{bmatrix} p_x \\ p_y \\ v_x \\ v_y \end{bmatrix}
\]
このベクトルに対して、行列を使って「予測」と「更新」を行います。ここで重要な概念が状態空間モデルです。
予測ステップ:物理法則を行列にする
高校物理で習う「距離 = 初期位置 + 速度 × 時間」という式を思い出してください。微小時間 $\Delta t$ 後の位置は次のように表せます。
\[
p_{x(t+1)} = p_{x(t)} + v_{x(t)} \cdot \Delta t
\]
速度が一定(等速直線運動)だと仮定すれば、速度の式は単純です。
\[
v_{x(t+1)} = v_{x(t)}
\]
これらを4つの要素すべてについて並べ、行列形式 \( \mathbf{x}_{new} = F \mathbf{x} \) で書くと、以下のようになります。これが状態遷移行列 $F$ です。
\[
\begin{bmatrix} p_x \\ p_y \\ v_x \\ v_y \end{bmatrix}_{t+1} =
\begin{bmatrix}
1 & 0 & \Delta t & 0 \\
0 & 1 & 0 & \Delta t \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1\\
\end{bmatrix}
\begin{bmatrix} p_x \\ p_y \\ v_x \\ v_y \end{bmatrix}_t
\]
この行列 \( F \) を掛けるだけで、物理法則に基づいた「未来の予測」が一瞬で計算できるのです。
更新ステップ:隠れ状態の推定
今回の設定では、センサ(GPSなど)は「X座標とY座標」しか教えてくれないとします。速度は直接測れません。このとき、状態ベクトルから観測値を取り出す観測行列 \(H\) は以下のようになります。
\[
H = \begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
\end{bmatrix}
\]
カルマン・フィルタの凄いところは、この「位置の観測」と「物理モデル(予測)」との間のズレ(残差)を利用して、直接測っていない「速度」の推定値まで修正してくれる点です。これを隠れ状態の推定と呼びます。
2. 実践編:Pythonで実装する2次元カルマン・フィルタ
それでは、Pythonでの実装に入りましょう。
AI開発でよく使われるNumPyを使用します。NumPyは行列演算に特化しており、数式をほぼそのままコードに落とし込めるため、カルマン・フィルタの実装に最適です。
ライブラリの準備
import numpy as np
import matplotlib.pyplot as plt
# 乱数シードを固定(再現性のため)
np.random.seed(42)カルマン・フィルタ・クラスの実装
汎用的に使えるよう、クラスとして実装します。数式に出てくる行列 $F, H, Q, R, P$ をメンバ変数として持ちます。
class KalmanFilter2D:
def __init__(self, dt, process_noise_std, measurement_noise_std):
"""
2次元等速運動モデル用カルマン・フィルタ
Parameters:
dt (float): 時間刻み
process_noise_std (float): プロセスノイズの標準偏差(モデルの不確かさ)
measurement_noise_std (float): 観測ノイズの標準偏差(センサの不確かさ)
"""
self.dt = dt
# 1. 状態ベクトル x = [px, py, vx, vy]^T
# 初期値はすべて0とする (4x1行列)
self.x = np.zeros((4, 1))
# 2. 状態遷移行列 F
# 位置 += 速度 * dt の関係を記述
self.F = np.array([
[1, 0, dt, 0],
[0, 1, 0, dt],
[0, 0, 1, 0],
[0, 0, 0, 1]
])
# 3. 観測行列 H
# 状態ベクトルのうち、位置(px, py)のみを観測する
self.H = np.array([
[1, 0, 0, 0],
[0, 1, 0, 0]
])
# 4. 誤差共分散行列 P
# 推定値の不確かさを表す。初期値は大きめに設定(最初は何もわかっていないため)
self.P = np.eye(4) * 1000.0
# 5. プロセスノイズの共分散行列 Q
# 「等速直線運動」というモデルがどれくらい現実とズレる可能性があるか。
# ここでは簡易的に対角行列で設定。実際は速度の変化などにノイズが乗る。
self.Q = np.eye(4) * (process_noise_std ** 2)
# 6. 観測ノイズの共分散行列 R
# センサの誤差分散。
self.R = np.eye(2) * (measurement_noise_std ** 2)
def predict(self):
"""
予測ステップ (Time Update)
x = Fx
P = FPF^T + Q
"""
# 状態の予測
self.x = self.F @ self.x
# 誤差共分散の予測
# @ は行列の積(ドット積)、.T は転置を表す
self.P = self.F @ self.P @ self.F.T + self.Q
return self.x
def update(self, z):
"""
更新ステップ (Measurement Update)
観測値 z を用いて予測を修正する
Parameters:
z (ndarray): 観測ベクトル [obs_x, obs_y]^T
"""
# 観測残差 y = z - Hx
y = z - (self.H @ self.x)
# 残差共分散 S = HPH^T + R
S = self.H @ self.P @ self.H.T + self.R
# カルマンゲイン K = PH^T S^-1
# np.linalg.inv で逆行列を計算
K = self.P @ self.H.T @ np.linalg.inv(S)
# 推定値の更新 x = x + Ky
self.x = self.x + (K @ y)
# 誤差共分散の更新 P = (I - KH)P
I = np.eye(self.P.shape[0])
self.P = (I - (K @ self.H)) @ self.P
return self.xコード解説
@演算子: Python 3.5以降およびNumPyでは、行列の積(ドット積)をA @ Bのように直感的に記述できます。np.linalg.inv(S): 行列 \(S\) の逆行列を求めます。ここがカルマンゲイン計算の肝です。- センサフュージョン:
updateメソッド内で、予測値(self.x)と観測値(z)が統合されています。
3. 実験編:見えない「速度」を捕まえる
実装したクラスを使って、シミュレーションを行ってみましょう。
「一定速度で斜めに移動する物体」を想定し、それにガウスノイズを加えた「観測データ」を作成します。カルマン・フィルタがノイズを除去し、さらに速度を正しく推定できるかを確認します。
シミュレーション用データの生成
# --- パラメータ設定 ---
dt = 0.1 # 時間刻み [s]
n_steps = 50 # ステップ数
measurement_std = 5.0 # 観測ノイズの標準偏差(位置の誤差)
process_std = 0.1 # プロセスノイズ(モデルの揺らぎ)
# --- 真の値(Ground Truth)の作成 ---
# 初期位置 (0, 0), 速度 (vx=2, vy=1) で等速移動
true_vx, true_vy = 2.0, 1.0
ground_truth = np.zeros((n_steps, 4)) # [px, py, vx, vy]
# 現在位置
cx, cy = 0.0, 0.0
for i in range(n_steps):
ground_truth[i] = [cx, cy, true_vx, true_vy]
cx += true_vx * dt
cy += true_vy * dt
# --- 観測値(Measurements)の作成 ---
# 真の位置にノイズを加える
# GPSなどは位置(x, y)しか観測できないと仮定
observations = ground_truth[:, :2] + np.random.normal(0, measurement_std, (n_steps, 2))フィルタリングの実行
# カルマン・フィルタのインスタンス化
kf = KalmanFilter2D(dt, process_std, measurement_std)
# 結果を格納するリスト
est_path = [] # 位置の推定結果
est_vel = [] # 速度の推定結果
# 最初の観測値で初期化(収束を早めるためのテクニック)
# ※必須ではありませんが、実用上よく行われます
kf.x[0, 0] = observations[0, 0]
kf.x[1, 0] = observations[0, 1]
# メインループ
for i in range(n_steps):
# 1. 予測ステップ
kf.predict()
# 現在の観測値を取得 (形状を (2, 1) に変形)
z = observations[i].reshape(2, 1)
# 2. 更新ステップ
kf.update(z)
# 結果を保存
est_path.append(kf.x[:2].flatten()) # 位置
est_vel.append(kf.x[2:].flatten()) # 速度
# NumPy配列に変換
est_path = np.array(est_path)
est_vel = np.array(est_vel)結果の可視化と分析
最後に、Matplotlibを使って結果をグラフ化します。ここでは「位置の軌跡」と「速度の推定推移」の2つを表示します。
fig, axes = plt.subplots(1, 2, figsize=(16, 6))
# --- グラフ1: 位置の軌跡 (X-Y平面) ---
ax1 = axes[0]
ax1.plot(ground_truth[:, 0], ground_truth[:, 1], 'g--', label='Ground Truth', linewidth=2)
ax1.scatter(observations[:, 0], observations[:, 1], c='gray', alpha=0.6, label='Observations (Noisy)')
ax1.plot(est_path[:, 0], est_path[:, 1], 'b-', label='Kalman Filter', linewidth=3)
ax1.set_title('Position Tracking (2D)')
ax1.set_xlabel('X [m]')
ax1.set_ylabel('Y [m]')
ax1.legend()
ax1.grid(True)
# --- グラフ2: 速度の推定推移 ---
ax2 = axes[1]
time_axis = np.arange(n_steps) * dt
ax2.axhline(y=true_vx, color='r', linestyle='--', label='True Vx (2.0)')
ax2.plot(time_axis, est_vel[:, 0], 'r-', label='Estimated Vx')
ax2.axhline(y=true_vy, color='c', linestyle='--', label='True Vy (1.0)')
ax2.plot(time_axis, est_vel[:, 1], 'c-', label='Estimated Vy')
ax2.set_title('Velocity Estimation (Hidden State)')
ax2.set_xlabel('Time [s]')
ax2.set_ylabel('Velocity [m/s]')
ax2.legend()
ax2.grid(True)
plt.show()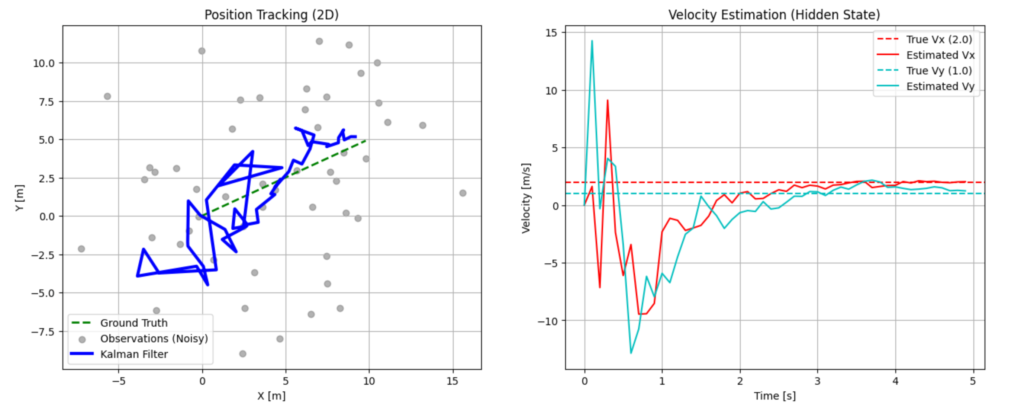
実行結果の考察
このコードを実行すると、2つのグラフが表示されます。
- 位置の軌跡: 灰色の点(観測値)はノイズにより上下左右に散らばっていますが、青い線(カルマン・フィルタ)は緑の点線(真の軌道)に沿って滑らかに移動していることがわかります。
- 速度の推定: ここが重要です。私たちは一度も速度計の値を入力していません。 しかし、右側のグラフを見ると、推定された速度(実線)が、真の速度(点線)に向かって収束していく様子が見て取れます。
なぜこれが可能なのか? それはカルマン・フィルタが「予測位置と観測位置のズレ」を分析し、「位置がこれだけ右にズレているということは、速度がもっと速いに違いない」と推論しているからです。これこそが、状態空間モデルにおける隠れ状態の推定の威力です。
4. 応用と発展:NumPyからPyTorchへ、そして非線形へ
今回はNumPyを使って実装しましたが、ディープラーニングフレームワークであるPyTorchやTensorFlowを使うとどうなるでしょうか?
実は、カルマン・フィルタの計算自体(行列の積や逆行列)は、PyTorchのテンソル演算(torch.matmul, torch.inverseなど)でそのまま置き換えることができます。
PyTorchを使う最大のメリットは、自動微分(Autograd)です。
今回、プロセスノイズ \(Q\) や観測ノイズ \(R\) の値は人間が手動で設定しました(これをチューニングと呼びます)。しかし、PyTorchを使えば、これらのパラメータ自体を「学習可能な変数」として扱い、実際のデータに合わせて最適な \(Q\) や \(R\) を勾配降下法で自動学習させるといった応用が可能になります。これは現代のAI・機械学習と従来の制御理論が交差する非常に面白い領域です。
次のステップ
今回のモデルは「等速直線運動(線形モデル)」でした。しかし、現実のロボットや車は急ハンドルを切ったり加速したりします。このような非線形な動きに対応するためには、拡張カルマン・フィルタ (EKF) や アンサンブル・カルマン・フィルタ (EnKF) といった発展的な手法が必要になります。
今回の2次元モデルの基礎が理解できていれば、それらの手法へのステップアップもスムーズなはずです。
おわりに
いかがでしたでしょうか。
「2次元への拡張」と聞くと難しそうに思えますが、NumPyによる行列演算を使えば、コード自体は非常にシンプルに記述できることを実感していただけたかと思います。
- 状態ベクトルで複数のパラメータ(位置・速度)をまとめて管理する。
- 行列演算で物理法則を一括処理する。
- 観測データから隠れた状態(速度)をあぶり出す。
この3つのポイントを押さえておけば、カルマン・フィルタはあなたの強力な武器になります。ぜひ、ご自身の手元のデータや、マウスカーソルの動きなどで遊んでみてください。
最後まで読んでいただきありがとうございました。



コメント