こんにちは、JS2IIUです。
これまで、「カルマン・フィルタ(KF)」によるノイズ除去、「拡張カルマン・フィルタ(EKF)」による非線形システムの追跡と、確率ロボティクスの王道とも言える技術を紹介してきました。
これらは非常に強力なツールですが、実はある一つの「呪縛」に囚われています。それは、「世界はガウス分布(正規分布)でできている」という思い込みです。
KFもEKFも、物体の位置を「平均値」と「分散(ボヤけ具合)」という2つのパラメータだけで表現しようとします。しかし、現実世界にはそれでは表現しきれない状況が存在します。
例えば、全く同じ形のドアが2つ並んでいる廊下を想像してください。ロボットが「目の前にドアがある」と認識したとき、ロボットがいる可能性がある場所は「ドアAの前」と「ドアBの前」の2箇所です。確率分布の山が2つある状態(多峰性分布)ですね。
これを無理やり1つのガウス分布で表そうとすると、平均値である「ドアAとドアBのちょうど中間(つまり壁の中)」を現在地として出力してしまいます。これでは使い物になりません。
そこで登場するのが、今回の主役「パーティクル・フィルタ(Particle Filter)」です。
パーティクル・フィルタは、難しい数式やヤコビ行列の計算を一切必要としません。代わりに必要なのは、「コンピュータの計算パワー」と「乱数」です。
「数式で解けないなら、シミュレーションで何千回も試して答えを出せばいいじゃない」という、ある意味で「数の暴力」とも言えるモンテカルロ法のアプローチ。その豪快かつ柔軟なアルゴリズムの世界へご案内します。今回もよろしくお願いします。
1. パーティクル・フィルタの概念:適者生存のシミュレーション
パーティクル・フィルタのアイデアは非常に直感的です。
「ロボットが今どこにいるか分からない」のなら、地図上に「ロボットの分身(粒子:パーティクル)」を数千個ばら撒いてしまえばいいのです。
この数千個の粒子一つひとつが、「私はここにいると思う」「いや、私はこっちだと思う」という仮説を持っています。これらの粒子に対して、以下の3つのステップを繰り返すことで、正解に近い粒子だけを残していきます。これはまるで生物の進化(適者生存)のようなプロセスです。
Step 1: 予測(Predict)― 全員で目隠し歩行
ロボットが「1メートル進んだ」とします。このとき、数千個の粒子すべてを同様に1メートル進めます。
ただし、ロボットの動きには誤差(ノイズ)があります。そこで、粒子ごとに少しずつ異なるランダムなノイズを加えて移動させます。これにより、粒子の分布は少し広がります。
Step 2: 計測・重み付け(Update / Weight)― 答え合わせ
次に、ロボットがセンサで周囲を観測します(例:「壁まで2メートル」)。
各粒子も、自分の仮説上の位置から「もしここにいたら、壁までは何メートルか?」を計算します。
- 粒子A:「私の位置なら、壁まで2.0メートルのはずだ」 → 実際の観測と一致! → 高得点(重み大)
- 粒子B:「私の位置だと、壁まで5.0メートルのはずだが…」 → 実際の観測とズレている → 低得点(重み小)
この点数のことを統計学用語で「尤度(ゆうど、Likelihood)」と呼びます。
Step 3: リサンプリング(Resample)― 自然淘汰
ここが最も重要なステップです。
点数(重み)に基づいて、粒子を選別します。
- 点数の高い粒子は、コピーして分裂し、数を増やします。
- 点数の低い粒子は、削除され消滅します。
これを繰り返すと、最初はバラバラだった粒子が、次第に「もっともらしい場所」だけに集まっていきます。これがパーティクル・フィルタによる位置推定の仕組みです。
2. Python実装:NumPyの「ブロードキャスト」で高速化する
それでは、Pythonで実装していきましょう。
パーティクル・フィルタの実装において最大の敵は「計算速度」です。数千個の粒子に対して for ループで一つずつ計算していては、日が暮れてしまいます。
そこで、Pythonの数値計算ライブラリNumPyの出番です。NumPyのブロードキャスト機能とベクトル化演算を駆使して、数千個の粒子を一括処理する方法を解説します。
ライブラリのインポート
import numpy as np
import matplotlib.pyplot as plt
import math
# 乱数シードの固定(再現性のため)
np.random.seed(42)パーティクル・フィルタ・クラスの実装
ロボットの状態を [x, y, yaw] (位置と向き)とし、これを N 個の粒子で管理するクラスを作成します。
class ParticleFilter:
def __init__(self, num_particles, map_limits):
"""
初期化
:param num_particles: 粒子の数(例: 1000個)
:param map_limits: [x_min, x_max, y_min, y_max] 粒子の散布範囲
"""
self.N = num_particles
# 1. 粒子の初期化 (一様分布でランダムにばら撒く)
# particles shape: (N, 3) -> [x, y, yaw]
x_min, x_max, y_min, y_max = map_limits
self.particles = np.zeros((self.N, 3))
self.particles[:, 0] = np.random.uniform(x_min, x_max, self.N) # x
self.particles[:, 1] = np.random.uniform(y_min, y_max, self.N) # y
self.particles[:, 2] = np.random.uniform(-np.pi, np.pi, self.N) # yaw (向き)
# 重みの初期化 (全員平等)
self.weights = np.ones(self.N) / self.N
def predict(self, velocity, yaw_rate, dt, std_v, std_yaw):
"""
予測ステップ (目隠し移動)
ロボットの制御入力に合わせて粒子を移動させる。
ただし、ノイズを加える。
"""
# 制御入力にノイズを付加する(各粒子ごとに異なるノイズ)
# shape: (N,)
v_noisy = velocity + np.random.normal(0, std_v, self.N)
omega_noisy = yaw_rate + np.random.normal(0, std_yaw, self.N)
# 粒子の移動 (対向2輪モデルの近似)
# update x: x + v * cos(yaw) * dt
self.particles[:, 0] += v_noisy * np.cos(self.particles[:, 2]) * dt
# update y: y + v * sin(yaw) * dt
self.particles[:, 1] += v_noisy * np.sin(self.particles[:, 2]) * dt
# update yaw: yaw + omega * dt
self.particles[:, 2] += omega_noisy * dt
# 角度を -pi ~ pi に正規化
self.particles[:, 2] = (self.particles[:, 2] + np.pi) % (2 * np.pi) - np.pi
def update(self, measurement, landmark_pos, std_meas):
"""
更新・重み付けステップ (尤度計算)
:param measurement: 観測されたランドマークまでの距離
:param landmark_pos: ランドマークの真の位置 [x, y]
:param std_meas: 計測ノイズの標準偏差
"""
# 全粒子の位置からランドマークまでの距離を計算 (ユークリッド距離)
# dx, dy shape: (N,)
dx = self.particles[:, 0] - landmark_pos[0]
dy = self.particles[:, 1] - landmark_pos[1]
dist_particles = np.sqrt(dx**2 + dy**2)
# 尤度(Likelihood)の計算
# ガウス分布の確率密度関数(PDF)を使って、「観測値とどれくらい近いか」を確率にする
# 観測値 measurement を中心としたガウス分布における、dist_particles の高さを求める
# P(z|x) = exp( - (z - pred)^2 / (2 * sigma^2) )
numerator = -(dist_particles - measurement)**2
denominator = 2 * (std_meas**2)
likelihood = np.exp(numerator / denominator)
# 重みの更新 (ゼロ除算回避のため微小値を足す)
self.weights = likelihood + 1.e-300
# 重みの正規化 (合計が1になるようにする)
self.weights = self.weights / np.sum(self.weights)
def resample(self):
"""
リサンプリング (自然淘汰)
重みに基づいて粒子を選び直す
"""
# 重みに比例した確率でインデックスをランダムに選ぶ
# np.random.choice は重み(p)を指定できる非常に便利な関数
indices = np.random.choice(self.N, size=self.N, p=self.weights)
# 選ばれたインデックスの粒子をコピーして新しい粒子集合とする
self.particles = self.particles[indices]
# 重みをリセット
self.weights = np.ones(self.N) / self.N
def estimate(self):
"""
現在の推定位置を計算 (粒子の平均値 or 最頻値)
"""
# 単純な平均で計算
x_est = np.mean(self.particles[:, 0])
y_est = np.mean(self.particles[:, 1])
yaw_est = np.arctan2(np.mean(np.sin(self.particles[:, 2])),
np.mean(np.cos(self.particles[:, 2])))
return np.array([x_est, y_est, yaw_est])コード解説:ここがポイント
- ベクトル化演算:
self.particles[:, 0] += ...のように書くことで、N個の粒子すべてに対して一度に計算を行っています。forループを使わないこの書き方が、Pythonでの数値計算を高速化する鉄則です。 - 尤度の計算:
updateメソッドでは、観測値と各粒子の予測値の差をガウス関数に入れて「もっともらしさ」を数値化しています。差が0に近いほど、expの結果(重み)は大きくなります。 np.random.choice: リサンプリングの核心部分です。重みが大きい粒子ほど選ばれる確率が高くなるルーレットを回すイメージです。
3. 実験:誘拐されたロボット問題
では、このクラスを使って実験を行いましょう。
今回は、確率ロボティクスにおける難問「誘拐されたロボット問題(Kidnapped Robot Problem)」、またの名を「大域的位置推定(Global Localization)」に挑戦します。
これは、「ロボットが地図上のどこにいるか全く分からない状態(初期位置不明)」からスタートし、移動と観測だけで自分の位置を特定できるか? という問題です。EKFでは初期位置を与えないと計算が発散してしまいますが、パーティクル・フィルタなら可能です。
シミュレーションの実行
# --- 設定 ---
num_particles = 1000
map_size = 20.0 # -10m ~ 10m
dt = 0.1
steps = 55
# 真のロボット (円運動させる)
true_x = -5.0 # スタート位置は適当
true_y = -5.0
true_yaw = 0.0
velocity = 1.0 # 1m/s
yaw_rate = 0.2 # 回転
# ランドマークの位置 (目印)
landmark = np.array([0.0, 0.0])
# PFのインスタンス化 (範囲 -10~10 にばら撒く)
pf = ParticleFilter(num_particles, [-10, 10, -10, 10])
# 可視化用のリスト
history_true = []
history_est = []
# --- ループ ---
for i in range(steps):
# 1. 真のロボットを移動
true_x += velocity * np.cos(true_yaw) * dt
true_y += velocity * np.sin(true_yaw) * dt
true_yaw += yaw_rate * dt
history_true.append([true_x, true_y])
# 2. 観測データの生成 (真の位置からランドマークまでの距離 + ノイズ)
dist_true = np.sqrt((true_x - landmark[0])**2 + (true_y - landmark[1])**2)
z = dist_true + np.random.normal(0, 0.5) # 観測ノイズ std=0.5
# 3. パーティクル・フィルタ実行
pf.predict(velocity, yaw_rate, dt, std_v=0.1, std_yaw=0.05)
pf.update(z, landmark, std_meas=0.5)
pf.resample()
# 推定値を保存
est = pf.estimate()
history_est.append(est)
# --- 可視化 (最初と最後だけ表示) ---
if i == 0 or i == 10 or i == steps - 1:
plt.figure(figsize=(6, 6))
plt.title(f"Step {i}")
# 粒子を描画
plt.scatter(pf.particles[:, 0], pf.particles[:, 1], s=2, c='blue', alpha=0.3, label='Particles')
# 真の位置
plt.scatter(true_x, true_y, c='red', marker='*', s=200, label='Ground Truth')
# 推定位置
plt.scatter(est[0], est[1], c='orange', marker='X', s=200, label='Estimate')
# ランドマーク
plt.scatter(landmark[0], landmark[1], c='black', marker='s', s=100, label='Landmark')
plt.xlim(-10, 10)
plt.ylim(-10, 10)
plt.legend()
plt.grid()
plt.show()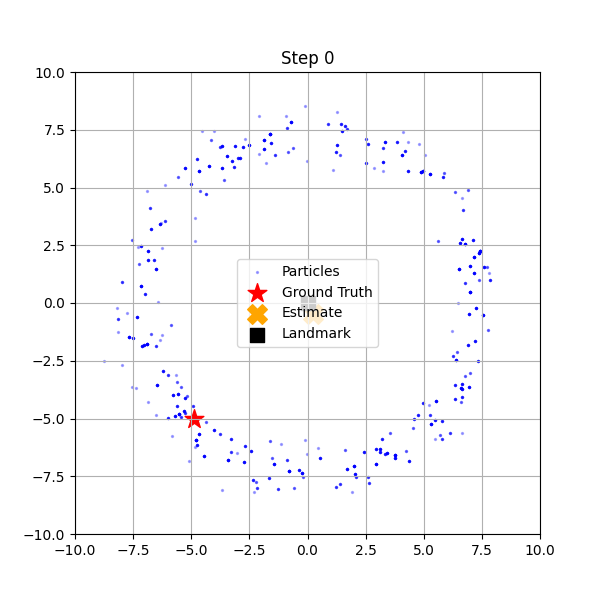
結果の解説
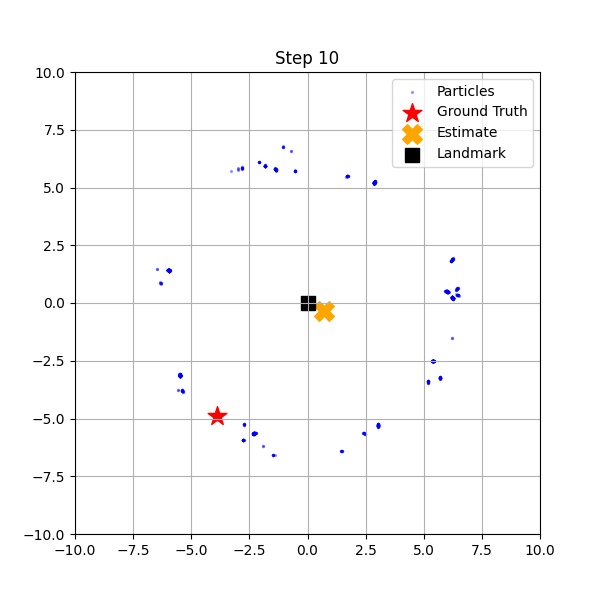
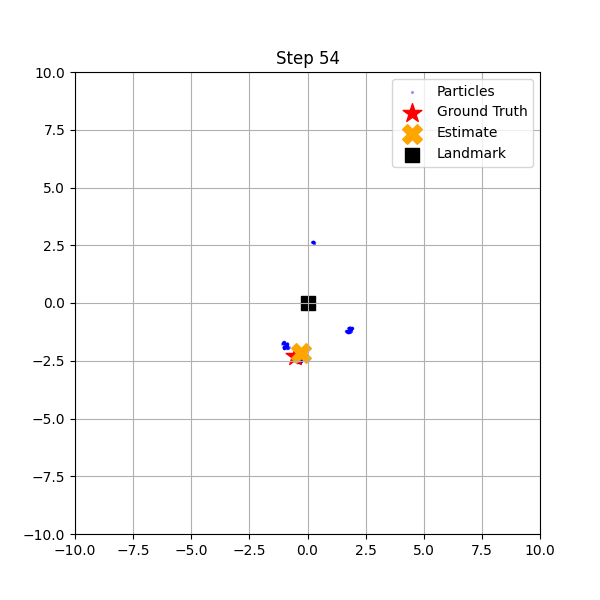
このコードを実行すると、3つのステップで粒子の様子が表示されます。
- Step 0 (初期状態):
青い点(粒子)が画面全体に均一に散らばっています。ロボットは自分がどこにいるか全くわかっていません。 - Step 10 (途中経過):
ロボットが移動し、ランドマーク(黒い四角)との距離を計測するたびに、距離が一致しない粒子が淘汰されていきます。その結果、粒子がドーナツ状(ランドマークから等距離の場所)や、特定のエリアに集まり始めます。 - Step 54 (最終状態):
粒子が赤い星(真のロボットの位置)の周りに密集しています! ロボットは「何も知らない状態」から、移動と観測を繰り返すだけで、自分自身の位置を特定することに成功しました。
これが大域的位置推定の成功です。EKFのような「一点の平均値」を追う手法では、最初の「全画面に散らばる」という表現ができないため、この芸当は不可能です。
まとめ:EKFとパーティクル・フィルタの使い分け
全3回にわたり、状態推定のアルゴリズムを見てきました。最後に、それぞれの特徴と使い分けを整理して締めくくりたいと思います。
| 特徴 | カルマン・フィルタ (KF/EKF) | パーティクル・フィルタ (PF) |
|---|---|---|
| 確率分布 | ガウス分布(平均と分散)に限定 | 自由(どんな形でもOK) |
| 非線形性 | 線形化(ヤコビ行列)で近似 | そのまま扱える(非線形OK) |
| 計算量 | 非常に軽い | 重い(粒子数に比例) |
| 実装難易度 | 数学(行列・微分)が必要 | 直感的(シミュレーション) |
| 得意なこと | 連続的な追跡、計算リソースの制約がある場合 | 初期位置不明からの復帰、複雑な地形での推定 |
結論:適材適所で使い分けよう
- 計算リソースが厳しく(組み込みマイコンなど)、ある程度初期位置が分かっているなら、EKFが最強の選択肢です。
- 計算パワーのあるGPUなどが使えて、予測不能な状況(誘拐問題など)に対応したいなら、パーティクル・フィルタが真価を発揮します。
現代のAI、特に自動運転やSLAM(自己位置推定と地図作成)の技術は、これらの基礎理論の上に成り立っています。「不確実な情報をどう扱うか」という視点は、ロボティクスに限らず、データサイエンス全般で役に立つはずです。
これでカルマン・フィルタ入門シリーズは完結です。ぜひ、ご自身の手でコードを動かし、確率の世界を楽しんでください!
最後まで読んでいただきありがとうございました。



コメント