こんにちは、JS2IIUです。
「1年後の株価はいくらになっているか?」
この問いに対して、ズバリ「12,500円です」と断言できる人は、預言者か詐欺師のどちらかでしょう。不確実な未来において、確実な一点を当てることは不可能です。
しかし、「1年後に株価が10,000円から13,000円の間に収まる確率は70%である」といった確率的な予測ならば、数学とコンピュータの力を使えば可能です。ここで登場するのがモンテカルロ法です。
今回は、金融工学の分野で基本となる「株価シミュレーション」を題材に、Pythonを使ってモンテカルロ法の実装を学びます。数式とコードを使って、無数の「あり得たかもしれない未来(パラレルワールド)」を生成し、その動きをアニメーション動画として可視化してみましょう。
理論背景:株価はどのように動くのか?
コードを書く前に、少しだけ理論の整理をしましょう。「デタラメに乱数を発生させれば株価の予測になる」わけではありません。それっぽい動きを作るためのモデルが必要です。
幾何ブラウン運動(GBM)
金融の世界では、株価の動きを表現するために幾何ブラウン運動(Geometric Brownian Motion: GBM)というモデルがよく使われます。名前は厳めしいですが、考え方はシンプルです。
ある瞬間の株価の変化は、以下の2つの要素の足し算で決まると考えます。
- ドリフト(Drift): 全体的なトレンド。例えば「年率5%で成長する」といった期待収益率に基づく上昇(または下降)圧力。
- 拡散(Diffusion): 予測不能なランダムな動き。日々のニュースや売買によるノイズ。
これを数式(確率微分方程式)で表すと以下のようになります。
$$ dS_t = \mu S_t dt + \sigma S_t dW_t $$
- \(S_t\): 株価
- \(\mu\) (ミュー): 期待収益率(ドリフト項の係数)
- \(\sigma\) (シグマ): ボラティリティ(変動率。拡散項の係数)
- \(dW_t\): ウィーナー過程(標準正規分布に従う乱数)
要するに、「基本的には金利や成長率に沿って増えていくが、その道中でサイコロを振ったようなランダムなブレが発生する」というモデルです。このモデルに基づいてシミュレーションを行うことで、現実の株価に近い動きを再現できます。
Pythonによる実装:シミュレーションエンジンの構築
それでは、Pythonで実装していきましょう。今回は、計算結果をただの数字の羅列で終わらせず、「時間が進むにつれて、株価の変動幅(リスク)がどう広がっていくか」を直感的に理解できるアニメーション動画として出力します。
使用ライブラリ
NumPy: 大量の乱数生成と行列演算による高速計算のため。Matplotlib: グラフ描画とアニメーション生成のため。
ソースコード全量
以下のコードは、設定したパラメータ(初期株価、ボラティリティなど)に基づき、200通り以上のシナリオを生成・描画します。Jupyter NotebookやローカルのPython環境で実行可能です。
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
# --- 1. シミュレーションの設定パラメータ ---
S0 = 10000 # 初期の株価 (円)
MU = 0.05 # 年率リターン (期待収益率 5%)
SIGMA = 0.20 # 年率ボラティリティ (変動率 20%)
T = 1.0 # 期間 (1年)
DAYS = 250 # 1年あたりの営業日数 (ステップ数)
SIMULATIONS = 200 # 生成するシナリオの数(パスの数)
# --- 2. データの生成 (幾何ブラウン運動モデル) ---
# 時間刻み幅 dt
dt = T / DAYS
# 乱数の生成
# 標準正規分布に従う乱数を (日数 x シミュレーション数) の行列で一括生成
np.random.seed(42) # 再現性のためシードを固定
Z = np.random.normal(0, 1, (DAYS, SIMULATIONS))
# 株価変動率(対数収益率)の計算
# 式: exp((mu - sigma^2 / 2) * dt + sigma * sqrt(dt) * Z)
drift = (MU - 0.5 * SIGMA**2) * dt
diffusion = SIGMA * np.sqrt(dt) * Z
daily_returns = np.exp(drift + diffusion)
# 累積積(cumprod)を使って株価パスを作成
# 初日(S0)をデータの先頭に追加するために vstack を使用
price_paths = np.vstack([np.ones((1, SIMULATIONS)), daily_returns])
price_paths = S0 * np.cumprod(price_paths, axis=0)
# 時間軸データ (0日目 〜 250日目)
time_axis = np.arange(DAYS + 1)
# --- 3. グラフとアニメーションの準備 ---
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))
fig.suptitle(f'Monte Carlo Simulation: Stock Price Prediction\n(S0={S0}, Volatility={SIGMA*100:.0f}%)', fontsize=16)
# 左側:株価パス(時系列グラフ)の設定
ax1.set_title("Stock Price Paths (Scenarios)")
ax1.set_xlabel("Days")
ax1.set_ylabel("Price (JPY)")
ax1.set_xlim(0, DAYS)
# グラフの縦軸範囲をデータの最大最小に合わせて調整
y_min = np.min(price_paths) * 0.9
y_max = np.max(price_paths) * 1.1
ax1.set_ylim(y_min, y_max)
ax1.grid(True, alpha=0.3)
# 描画用オブジェクトの初期化
# 複数の線を管理するためのリスト
lines = []
for _ in range(SIMULATIONS):
# 透明度(alpha)を下げて、線が重なった部分の密度を表現
line, = ax1.plot([], [], lw=1, alpha=0.2, color='blue')
lines.append(line)
# 平均値ライン(赤色太線)
line_mean, = ax1.plot([], [], 'r-', lw=2.5, label='Mean Price')
ax1.legend(loc='upper left')
# 情報表示用テキスト
info_text = ax1.text(0.02, 0.95, '', transform=ax1.transAxes,
bbox=dict(facecolor='white', alpha=0.8))
# 右側:価格分布(ヒストグラム)の設定
ax2.set_title("Price Distribution")
ax2.set_xlabel("Price (JPY)")
ax2.set_ylabel("Frequency")
ax2.set_xlim(y_min, y_max)
ax2.grid(True, alpha=0.3)
# 平均値ライン(縦線)
line_hist_mean = ax2.axvline(S0, color='r', linestyle='--', linewidth=2, label='Mean')
# --- 4. アニメーション更新関数 ---
def update(frame):
# 描画速度調整: 2フレームごとに進める
current_day = frame * 2
if current_day > DAYS:
current_day = DAYS
# --- 左グラフの更新 ---
# 現在の時点までのデータをセット
x_data = time_axis[:current_day+1]
# 全シナリオの線を更新
for i, line in enumerate(lines):
line.set_data(x_data, price_paths[:current_day+1, i])
# 平均値ラインの更新
mean_path = np.mean(price_paths[:current_day+1], axis=1)
line_mean.set_data(x_data, mean_path)
# テキスト更新
current_mean = mean_path[-1]
info_text.set_text(f'Day: {current_day}\nMean Price: {current_mean:.0f}')
# --- 右グラフの更新 ---
ax2.cla() # ヒストグラムは全描き直しが必要なのでクリア
# 設定の再適用
ax2.set_title(f"Price Distribution at Day {current_day}")
ax2.set_xlabel("Price (JPY)")
ax2.set_xlim(y_min, y_max)
ax2.set_ylim(0, SIMULATIONS / 3) # 高さを固定して見やすくする
ax2.grid(True, alpha=0.3)
# その時点での全シナリオの株価を取得
current_prices = price_paths[current_day]
# ヒストグラム描画
ax2.hist(current_prices, bins=30, color='skyblue', edgecolor='black', alpha=0.7)
# 平均値ラインの再描画
ax2.axvline(current_mean, color='r', linestyle='--', linewidth=2, label=f'Mean: {current_mean:.0f}')
ax2.legend(loc='upper right')
# 更新されたオブジェクトを返す(今回はblit=Falseなので必須ではないが慣例として)
return lines + [line_mean, info_text]
# --- 5. 動画の保存と実行 ---
print("アニメーション生成中...(数分かかる場合があります)")
# フレーム数を計算
frames_count = DAYS // 2 + 1
ani = FuncAnimation(fig, update, frames=frames_count, interval=30, blit=False)
# 保存処理
try:
# ffmpegがインストールされている場合、mp4で保存
ani.save('stock_simulation.mp4', writer='ffmpeg', fps=30)
print("保存完了: stock_simulation.mp4")
except Exception as e:
print(f"MP4保存エラー: {e}")
print("GIFとして保存を試みます...")
# 失敗した場合(ffmpegがない場合など)はGIFで保存
ani.save('stock_simulation.gif', writer='pillow', fps=30)
print("保存完了: stock_simulation.gif")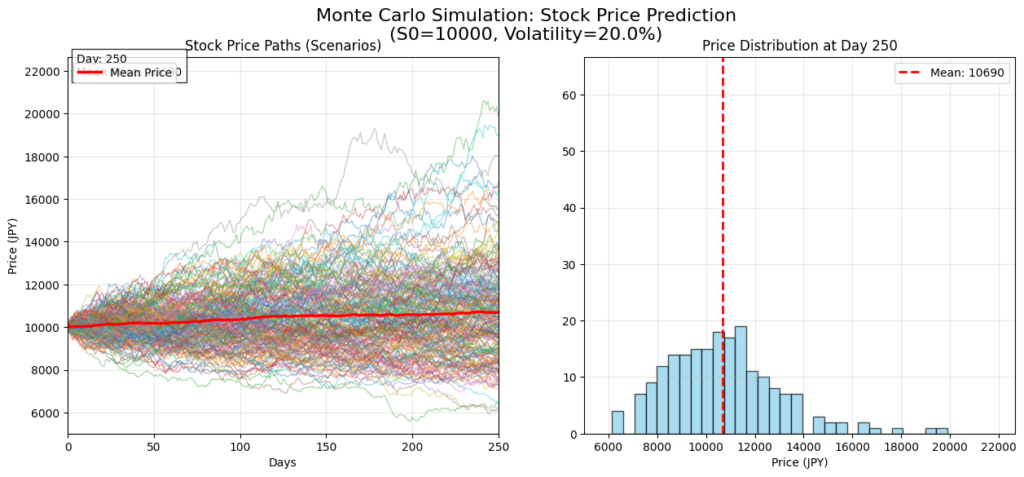
コードの技術的詳細解説
このプログラムの肝となる部分を詳しく見ていきましょう。
1. NumPyによるベクトル演算(高速化の鍵)
シミュレーションで最も重要なのは計算速度です。for文を使って「1日ずつ、1シナリオずつ」計算すると、Pythonでは非常に遅くなってしまいます。
そこで、NumPyの行列計算(ベクトル化)を活用しています。
# 悪い例(遅い)
# for t in range(DAYS):
# for s in range(SIMULATIONS):
# ...
# 良い例(今回の実装)
Z = np.random.normal(0, 1, (DAYS, SIMULATIONS))このように (日数, シミュレーション数) の大きさを持つ乱数の行列を一気に作り、計算式をそのまま適用することで、何万回もの計算を瞬時に終わらせることができます。
2. 累積積(cumprod)によるパス生成
日々の「変化率(リターン)」が計算できたら、それを積み上げて実際の「株価」にする必要があります。ここでは np.cumprod(累積積)を使っています。
- 1日目:\(S_0 \times r_1\)
- 2日目:\(S_0 \times r_1 \times r_2\)
- 3日目:\(S_0 \times r_1 \times r_2 \times r_3\) …
という計算を一発で行ってくれます。これにより、複利効果を含んだ株価の推移パスが生成されます。
3. Matplotlibのアニメーション
FuncAnimation は、フレームごとに update 関数を呼び出し、グラフの状態を少しずつ変化させることで動画を作ります。
今回は、右側のヒストグラム(分布図)の変化が重要です。ax2.cla() で一度グラフを消去し、その時点での株価データを使ってヒストグラムを描き直すことで、「最初は一点に集中していた分布が、時間の経過とともに平たく広がっていく様子」を表現しています。
実行結果の読み解き方
プログラムを実行して生成された動画を見てみましょう。ここには、金融工学の重要な概念が視覚的に表れています。
左のグラフ:リスクの拡大
スタート地点(Day 0)では、全てのシナリオが現在の株価(10,000円)にいます。しかし、時間が経つにつれてシナリオごとの格差が広がっていきます。
グラフ全体がラッパのような形に広がっていく様子が見て取れるはずです。この「ラッパの広がり幅」こそが、将来の不確実性(リスク)そのものです。
右のグラフ:分布の形状
右側のヒストグラムを見ると、最初は一本の棒ですが、徐々に山なりに広がっていきます。
ここで注目すべきは、分布が左右対称ではなく、左側(安い方)が詰まっていて、右側(高い方)に裾が長い形になっている点です。
これを対数正規分布と呼びます。株価は決してマイナスにならない(0円で止まる)一方で、上昇方向には理論上上限がないため、このような形になります。
実務への応用:単なる予測を超えて
モンテカルロ法は、単に「将来の株価」を眺めて楽しむためのものではありません。実務では以下のような意思決定に使われます。
1. バリュー・アット・リスク(VaR)の計算
「最悪の場合、どれくらい損をする可能性があるか?」を知りたいときに使います。
例えば、シミュレーション結果の下位5%のラインを見ることで、「95%の確率で、損失はこの金額以内に収まる」といったリスク管理の指標を算出できます。
2. オプション価格の評価
「1年後に株価が12,000円を超えていたら、その差額をもらえる権利」のような金融派生商品(オプション)の価格を決める際、数式(ブラック・ショールズ式)で解くのが難しい複雑な条件でも、モンテカルロ法ならシミュレーションの平均値を取るだけで適正価格を算出できます。
まとめ
本記事では、モンテカルロ法を使って株価の動きをシミュレーションし、その結果をPythonで可視化する方法を解説しました。
- モンテカルロ法は、乱数を使って不確実な未来の「分布」を知るための手法。
- 幾何ブラウン運動モデルを使えば、リアルな株価変動を再現できる。
- PythonとNumPyを使えば、複雑な確率計算も数行のコードで高速に処理できる。
- 可視化することで、「リスク(不確実性)」が時間とともにどう増幅するかを直感的に理解できる。
プログラミングにおいて、確定的なアルゴリズムだけでなく、このような「確率的なアプローチ」を身につけると、解決できる問題の幅が劇的に広がります。ぜひ、パラメータ(ボラティリティや期間)を変えて実験し、確率の世界を楽しんでみてください。
最後まで読んでいただきありがとうございます。



コメント