こんにちは、JS2IIUです。
朝の通勤ラッシュ、駅のホームや改札での人の流れを観察したことはあるでしょうか?
一見すると混沌としているように見えますが、そこには「ぶつからないように避ける」「空いている場所を探す」「目的地へ向かう」という、個々人のミクロな意思決定の積み重ねが存在しています。
こうした現象をコンピュータ上で再現し、混雑の緩和や防災計画に役立てる技術がマルチエージェントシミュレーション(MAS)です。専用の解析ソフトは高価なものが多いですが、実はPythonと基本的な物理法則の知識があれば、私たちエンジニアも独自にシミュレーションモデルを構築することが可能です。
本記事では、物理学のアプローチを応用した社会力モデル(Social Force Model)を用いて、駅の自動改札を通過する群衆の動きをシミュレーションします。また、シミュレーション開発で必ずと言っていいほど直面する「エージェントが壁際で動かなくなる(デッドロック)」問題の技術的な解決策についても解説します。今回もよろしくお願いします。
理論編:群衆を物理学で解く「社会力モデル」
人の動きをコードに落とし込む際、最も直感的で広く使われているアルゴリズムの一つが「社会力モデル(Social Force Model)」です。
このモデルの核心は、「人間を物理的な力の影響を受ける粒子(エージェント)として扱う」という点にあります。もちろん、実際に人が磁石のように引き合ったり反発したりしているわけではありませんが、心理的な働きを「仮想的な力」として数式化することで、驚くほどリアルな挙動を再現できます。
エージェント (i) に働く力 $F_i$ は、主に以下の3つの要素の合計で表されます。
- 目的地への引力 (Driving Force):
「改札を通りたい」「出口へ向かいたい」という意志です。現在の速度ベクトルを、目的方向への希望速度に近づける力として計算します。 - 他人からの斥力 (Social Repulsion):
「他人とぶつかりたくない」「パーソナルスペースを確保したい」という心理的・物理的な反発力です。相手との距離が近くなるほど、指数関数的に強い力が働きます。 - 壁からの斥力 (Wall Repulsion):
壁や障害物を避ける力です。
これらの力を合計し、ニュートンの運動方程式(\(F=ma\))に基づいて加速度を算出します。そして、オイラー法(Euler Method)などの数値積分法を用いて、微小時間 \(\Delta t\) ごとの速度と位置を更新していくのが基本的な仕組みです。
実装編:駅の自動改札をモデリングする
では、実際にPythonを使って実装していきましょう。数値計算にはNumPyを、可視化にはMatplotlibを使用します。
特にNumPyは、位置座標 \((x, y)\) や速度ベクトル \((v_x, v_y)\) を配列として高速に処理できるため、多数のエージェントを扱うMASには必須のライブラリです。
環境設定とエージェントの定義
シミュレーション空間は、左側から人が流入し、中央にある「壁(改札機)」の隙間(ゲート)を通って右側へ抜ける構造とします。
ここで重要になるのが、エージェントがどのように動くかを計算する update メソッドです。以下のようなベクトル計算が基本となります。
# 現在地から目的地へのベクトルを計算
direction = target_pos - self.pos
dist_target = np.linalg.norm(direction)
# 正規化(単位ベクトル化)
if dist_target > 0:
direction /= dist_target
# 希望する速度ベクトル
desired_vel = direction * self.max_speed
# 力の計算 F = (希望速度 - 現在速度) / 反応時間
force = (desired_vel - self.vel) / 0.5このように、NumPyの線形代数モジュール np.linalg を活用することで、複雑な三角関数を書くことなく、ベクトル演算だけで「向き」や「距離」を扱うことができます。
課題解決編:シミュレーションの「壁」を乗り越える
単純に「目的地へ向かう力」と「障害物を避ける力」を実装しただけでは、多くの場合、シミュレーションはうまくいきません。特に狭い通路や部屋の角などで、エージェント同士がお見合いをしてしまったり、壁に向かって押し続けたりするデッドロック(Deadlock)が発生します。
ここでは、より人間に近い挙動を実現するために導入した3つの技術的アプローチを紹介します。
1. ウェイポイント(Waypoint)による整列
現実の改札では、人は斜めから改札機に突っ込むことはしません。少し手前で一旦列に並び、正面から進入しようとします。
これを再現するために、ウェイポイント(経由地)の概念を導入します。
- 改札から遠い場合 \(\rightarrow\) 「改札の手前1.5m」を目指す
- 改札の手前に着いた場合 \(\rightarrow\) 「改札の奥」を目指す
このように状態に応じて目的地を切り替えることで、エージェントは自然と改札前で「整列」するような動きを見せるようになります。
2. ウォールスライディング(Wall Sliding)
物理シミュレーションにおいて、壁に向かって進もうとする力が、壁からの反発力と真正面から衝突すると、力が釣り合って動けなくなります。
現実の人間は、壁にぶつかったら「壁沿いに横にずれて」隙間を探そうとします。これをウォールスライディングとして実装します。
# 壁からの法線ベクトル(跳ね返す方向)
normal = diff / dist
# 接線ベクトル(壁沿いの方向): 法線を90度回転させる
# [x, y] -> [-y, x]
tangent = np.array([-normal[1], normal[0]])
# 進行方向成分を取り出し、接線方向への力を加える
force += tangent * np.dot(self.vel, tangent) * 5.0この処理を加えることで、エージェントは壁に張り付くことなく、ズルズルと壁沿いを移動してゲートへ吸い込まれるようになります。
3. ランダムノイズの付加
完全に力が均衡してしまう状態を防ぐため、計算の最後に微小なランダムな力(ノイズ)を加えます。これにより、膠着状態が自然に解消されるきっかけを作ります。
完成コードと可視化
これまでのロジックを統合した完全なコードが以下になります。
進捗状況がわかるようにTqdmライブラリを導入し、Matplotlibのアニメーション機能で動画として保存できるようにしています。
※このコードを実行するには numpy, matplotlib, tqdm が必要です。動画保存には ffmpeg が推奨されますが、ない場合はGIFとして保存されます。
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from matplotlib.patches import Rectangle
import random
from tqdm import tqdm
# --- 設定パラメータ ---
NUM_AGENTS = 60 # エージェント数
WIDTH, HEIGHT = 20, 10 # フィールドサイズ (メートル)
GATE_X = 10.0 # 改札のX座標
GATE_WIDTH = 0.8 # 通路幅
WALL_THICKNESS = 0.5 # 壁厚
GATE_POSITIONS = [2.5, 5.0, 7.5] # 改札通路のY座標
SIM_DURATION = 400 # シミュレーションステップ数
DT = 0.1 # タイムステップ (秒)
# --- エージェントクラス ---
class Agent:
def __init__(self, id):
self.id = id
# 初期位置:左側のエリアにランダム配置
self.pos = np.array([random.uniform(0, 5), random.uniform(0, HEIGHT)])
self.vel = np.array([0.0, 0.0])
self.radius = 0.3 # 人の半径
# 歩行速度に個人差を持たせる
self.max_speed = 1.3 + random.uniform(-0.3, 0.3)
self.target_gate_idx = self.select_nearest_gate()
self.color = np.random.rand(3,)
def select_nearest_gate(self):
"""最も近いゲートを選択する"""
dists = [abs(self.pos[1] - gy) for gy in GATE_POSITIONS]
return np.argmin(dists)
def update(self, agents, walls):
"""力の計算と位置更新を行うメインロジック"""
# --- 1. 目的地への引力 (Driving Force) ---
gate_y = GATE_POSITIONS[self.target_gate_idx]
# 【重要】ウェイポイントロジック
if self.pos[0] < GATE_X - 1.5:
# 改札の手前1.5mまでは「整列ライン」を目指す
target_pos = np.array([GATE_X - 1.0, gate_y])
speed_limit = self.max_speed
elif self.pos[0] < GATE_X + WALL_THICKNESS:
# 整列後はゲートの向こう側を目指す
target_pos = np.array([GATE_X + 2.0, gate_y])
# ゲート内通過時の減速処理 (ICカードタッチ等を想定)
if GATE_X - 0.5 < self.pos[0] < GATE_X + 0.5:
if abs(self.pos[1] - gate_y) < GATE_WIDTH:
speed_limit = 0.6
else:
speed_limit = 0.3 # 詰まっている時
else:
speed_limit = self.max_speed
else:
# 通過後は出口(右端)へ
target_pos = np.array([WIDTH + 2, self.pos[1]])
speed_limit = self.max_speed
direction = target_pos - self.pos
dist_target = np.linalg.norm(direction)
if dist_target > 0:
direction /= dist_target
# 自分の意思で進もうとする力
desired_vel = direction * speed_limit
force = (desired_vel - self.vel) / 0.5 # 0.5秒で反応
# --- 2. 他のエージェントからの斥力 (Social Repulsion) ---
for other in agents:
if other.id != self.id:
diff = self.pos - other.pos
dist = np.linalg.norm(diff)
safe_dist = self.radius + other.radius + 0.1
if dist < safe_dist:
# 距離が近いほど強く反発する
repulsion_strength = 2000.0 * np.exp(-(dist / 0.5))
force += (diff / dist) * repulsion_strength
# --- 3. 壁からの斥力 (Wall Repulsion) ---
for wall in walls:
wx_min, wx_max = wall['x']
wy_min, wy_max = wall['y']
# クランプ処理で壁上の最近接点を計算
closest_x = max(wx_min, min(self.pos[0], wx_max))
closest_y = max(wy_min, min(self.pos[1], wy_max))
closest_pt = np.array([closest_x, closest_y])
diff = self.pos - closest_pt
dist = np.linalg.norm(diff)
if dist < self.radius + 0.2:
if dist > 0:
force += (diff / dist) * 100.0 * (self.radius + 0.2 - dist)
# 【重要】ウォールスライディング (Wall Sliding)
# 壁の法線ベクトル
normal = diff / dist
# 接線ベクトル(法線を90度回転)
tangent = np.array([-normal[1], normal[0]])
# 進行方向成分を接線方向に加算して「滑り」を再現
force += tangent * np.dot(self.vel, tangent) * 5.0
else:
# めり込み回避
force += np.array([-1.0, 0]) * 200
# --- 4. デッドロック回避用のノイズ ---
force += np.random.normal(0, 2.0, 2)
# --- オイラー法による積分 ---
self.vel += force * DT
speed = np.linalg.norm(self.vel)
if speed > speed_limit: # 速度制限
self.vel = (self.vel / speed) * speed_limit
self.pos += self.vel * DT
# --- 環境(壁)の定義 ---
walls = []
# 外枠
walls.append({'x': [-1, WIDTH+1], 'y': [-1, 0]})
walls.append({'x': [-1, WIDTH+1], 'y': [HEIGHT, HEIGHT+1]})
# 改札機(ゲート間の壁)
prev_y = 0
for gy in GATE_POSITIONS:
lower_y = gy - GATE_WIDTH / 2
walls.append({'x': [GATE_X, GATE_X + WALL_THICKNESS], 'y': [prev_y, lower_y]})
prev_y = gy + GATE_WIDTH / 2
walls.append({'x': [GATE_X, GATE_X + WALL_THICKNESS], 'y': [prev_y, HEIGHT]})
# --- シミュレーション実行 ---
agents = [Agent(i) for i in range(NUM_AGENTS)]
history = []
print("シミュレーション計算中...")
# Tqdmでプログレスバーを表示
for t in tqdm(range(SIM_DURATION), desc="Step"):
frame_data = []
for agent in agents:
agent.update(agents, walls)
frame_data.append(agent.pos.copy())
history.append(frame_data)
# --- 可視化と動画保存 ---
fig, ax = plt.subplots(figsize=(10, 5))
ax.set_xlim(0, WIDTH)
ax.set_ylim(0, HEIGHT)
ax.set_title("駅自動改札の人流シミュレーション")
ax.set_xlabel("距離 (m)")
ax.set_ylabel("距離 (m)")
# 壁の描画
for wall in walls:
w = wall['x'][1] - wall['x'][0]
h = wall['y'][1] - wall['y'][0]
rect = Rectangle((wall['x'][0], wall['y'][0]), w, h, color='gray')
ax.add_patch(rect)
# 整列ラインのガイド表示
ax.axvline(x=GATE_X - 1.5, color='green', linestyle=':', alpha=0.3, label="整列開始ライン")
ax.legend(loc='upper right')
# エージェントの描画オブジェクト
scat = ax.scatter([], [], c=[], s=50, cmap='jet', vmin=0, vmax=2.0, edgecolor='black')
def animate(i):
positions = np.array(history[i])
scat.set_offsets(positions)
# 速度に応じて色を変える(速いと赤、遅いと青)
if i > 0:
prev_pos = np.array(history[i-1])
speeds = np.linalg.norm(positions - prev_pos, axis=1) / DT
scat.set_array(speeds)
ax.set_title(f"Time: {i*DT:.1f} s")
return scat,
ani = animation.FuncAnimation(fig, animate, frames=len(history), interval=30, blit=True)
print("動画保存中...")
# 動画保存時もプログレスバーを表示するためのコールバック
pbar = tqdm(total=len(history), unit="frame")
def progress_callback(c, t):
pbar.update(1)
try:
# FFmpegがインストールされていればmp4で保存
ani.save("simulation_flow.mp4", writer="ffmpeg", fps=30, progress_callback=progress_callback)
print("保存完了: simulation_flow.mp4")
except Exception:
# なければGIFで保存
ani.save("simulation_flow.gif", writer="pillow", fps=30, progress_callback=progress_callback)
print("保存完了: simulation_flow.gif")
pbar.close()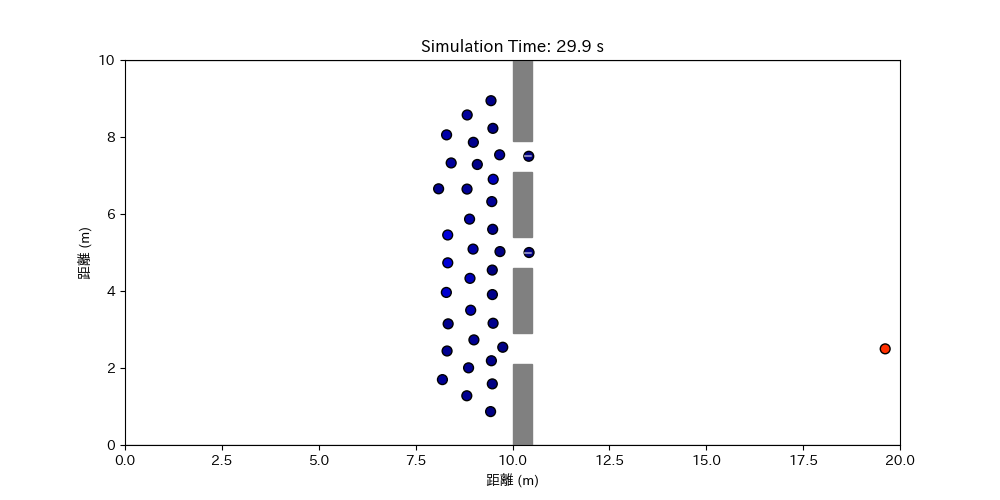
コードのポイント
Agent.update: ここに全ての物理演算が集約されています。引力、他人からの斥力、壁からの斥力(+スライディング)を合算し、次の位置を決定します。numpy.linalg.norm: 2点間の距離や速度の大きさ(スカラー)を求めるために多用しています。tqdm: シミュレーション計算と動画エンコードは時間がかかる処理ですが、プログレスバーがあることで安心して待つことができます。
おわりに
今回は、Pythonの基本的なライブラリを使って、ルールベースの「社会力モデル」によるシミュレーションを実装しました。ウェイポイントや壁ずり処理といった工夫を加えることで、デッドロックを回避し、人間らしいスムーズな流れを表現できることが確認できたかと思います。
本記事では物理法則に基づいたルールを手動で記述しましたが、近年では機械学習、特に深層強化学習(Deep Reinforcement Learning)を用いて、エージェント自身に「どう動けば効率的か」を学習させるアプローチも研究されています。
その場合、今回実装したような環境(Environment)を構築し、PyTorchなどのフレームワークを使ってエージェントの脳(ニューラルネットワーク)をトレーニングすることになります。
シミュレーションの世界は奥が深く、少しのパラメータ変更で全く異なる結果が得られます。ぜひパラメータを変えたり、改札の数を増やしたりして、独自の実験を楽しんでみてください。
最後まで読んでいただきありがとうございます。



コメント