こんにちは、JS2IIUです。
前回の記事では、物理学の「力」の概念を応用した社会力モデル(Social Force Model)を使って、駅の改札を通る人々の物理的な動きをシミュレーションしました。
しかし、前回のシミュレーションには一つ、現実とは大きく異なる点がありました。それは、エージェント(登場人物)たちが「思考停止して一番近い改札に突っ込んでいく」という点です。
現実ではいくつかの判断基準でどの列に並ぶかを決めています。スーパーマーケットでどのレジに並ぶかを考えている時のイメージです。今回は、この「状況を見て判断する(=賢い)」ロジックをPythonコードで実装していきます。
これによって、特定の改札に人が集中するのを防ぐ負荷分散(Load Balancing)が自然発生的に行われるようになります。単なる物理計算から、AIやアルゴリズムに近い領域へと踏み込んでいきましょう。
【参考】前回記事「マルチエージェントシミュレーション入門:NumPyとMatplotlibによる群衆挙動の実装」
https://js2iiu.com/2025/12/13/mullti-agent-simulation/
アルゴリズム設計:人間はどうやって列を選ぶのか?
コードを書く前に、私たち人間が無意識に行っている判断プロセスを数式化(モデリング)してみましょう。
スーパーのレジや駅の改札で並ぶ列を選ぶとき、私たちは主に2つの要素を天秤にかけています。
- 移動距離: そこまで歩くのがどれくらい面倒か。
- 待ち時間: 前に何人並んでいるか。
これをコスト関数(Cost Function)として定義します。人間は無意識に、このコストが最小になる選択肢を選ぼうとします。これをヒューリスティック(発見的手法)と呼びます。厳密な待ち時間を計算するのではなく、「行列が長い=遅いだろう」という経験則に基づく判断です。
数式で表すと以下のようになります。
$$ Cost = Distance + (QueueSize \times PatienceFactor) $$
- Distance: 現在地からそのゲートまでの距離
- QueueSize: そのゲートに並んでいる人数(の推定値)
- PatienceFactor: 「待つくらいなら歩く」という個人の性格(気の短さ)係数
この係数 \(PatienceFactor\) が大きければ大きいほど、その人は混雑を嫌って遠くの空いている改札を選ぼうとします。逆に小さければ、混んでいても近い改札を選びます。
実装フェーズ1:エージェントに「目」と「判断力」を与える
それでは、PythonとNumPyを使って実装していきましょう。
ベースとなるのは前回の Agent クラスですが、今回はこれを拡張して SmartAgent クラスを作成します。
まずは、「どの改札を選ぶべきか」を計算するメソッドを追加します。
class SmartAgent:
def __init__(self, id):
# ...(初期化処理は前回と同様)...
# ★ 思考用パラメータ
self.patience_factor = random.uniform(2.0, 4.0) # 気の短さ係数
def get_gate_cost(self, gate_idx, agents):
"""
ゲートを選択するためのコスト関数
Cost = (ゲートへの距離) + (行列の長さによるペナルティ)
"""
gate_y = GATE_POSITIONS[gate_idx]
gate_pos = np.array([GATE_X, gate_y])
# 1. 物理的な距離の計算
dist = np.linalg.norm(gate_pos - self.pos)
# 2. 混雑具合(行列の長さ)の推定
# 知覚(Perception)プロセス:自分より前にいる人をカウントする
queue_count = 0
for other in agents:
if other.id != self.id:
# 同じゲートを目指しているか?
if getattr(other, 'target_gate_idx', -1) == gate_idx:
# 自分よりゲートに近いか? (X座標で簡易判定)
# かつ、ゲートの手前5m以内にいるか?
if GATE_X - 5.0 < other.pos[0] < GATE_X:
if other.pos[0] > self.pos[0]:
queue_count += 1
# コスト計算
return dist + (queue_count * self.patience_factor)コードの解説
ここでのポイントは、知覚(Perception)の実装です。
現実の人間は、全ての改札の正確な待機人数を神の視点で知ることはできません。あくまで「自分の目に見える範囲」で判断します。
上記のコードでは、for ループを使って他のエージェントを確認し、「自分と同じゲートを目指していて、かつ自分より前にいる人」をカウントしています。これが簡易的な「行列の長さ」の推定値となります。
このカウント数に patience_factor を掛け合わせることで、混雑に対する心理的な抵抗感を数値化しています。
実装フェーズ2:非同期な意思決定と行動への反映
次に、計算したコストに基づいて行動を変更するロジックを実装します。ここで重要なのがリターゲティング(Retargeting)と非同期な意思決定(Asynchronous Decision Making)です。
もし、全エージェントが「毎フレーム(0.1秒ごと)」一斉に判断を行ったらどうなるでしょうか?
- 右のゲートが空いたと判断し、全員が右へ殺到する。
- 右が混雑したため、次の瞬間に全員が左へ殺到する。
このように、集団が左右に激しく揺れ動く「振動現象」が発生してしまいます。これを防ぐために、判断のタイミングをあえて分散させます。
class SmartAgent:
# ...(前述のinit続き)...
def __init__(self, id):
# ...
# 何ステップごとに考え直すか(全員同時だと不自然になるため分散)
self.decision_interval = random.randint(5, 15)
def think_best_gate(self, agents):
"""
最もコスト(距離+混雑)が低いゲートを選び直す
"""
costs = []
for i in range(len(GATE_POSITIONS)):
costs.append(self.get_gate_cost(i, agents))
# 最もコストが低いゲートのインデックスを返す
return np.argmin(costs)
def update(self, step_count, agents, walls):
# ★ 定期的に進路を再考する (Retargeting)
# 改札を通過する前(GATE_Xより手前)のみ考える
if self.pos[0] < GATE_X - 0.5:
# 自分の判断タイミングが来たときだけ思考する
if step_count % self.decision_interval == 0:
self.target_gate_idx = self.think_best_gate(agents)
# --- 以下、前回の物理挙動コードと同様 ---
# 目的地への移動ベクトル計算や衝突回避などdecision_interval をランダムに設定することで、エージェントはそれぞれ異なるタイミングで周囲を見回し、進路変更を行います。これにより、システム全体として滑らかな負荷分散が実現されます。
シミュレーション実行:賢くなった群衆の挙動
それでは、これらを統合した全体のコードを実行してみましょう。
今回は可視化の際、エージェントが「どのゲートを狙っているか」で色を変えるようにしました(上=赤、中=緑、下=青)。これにより、途中で色が変わり、考えを変えた瞬間が視覚的に分かります。
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from matplotlib.patches import Rectangle
import random
from tqdm import tqdm
# --- 設定パラメータ ---
NUM_AGENTS = 60
WIDTH, HEIGHT = 20, 10
GATE_X = 10.0
GATE_WIDTH = 0.8
WALL_THICKNESS = 0.5
GATE_POSITIONS = [2.5, 5.0, 7.5]
SIM_DURATION = 400
DT = 0.1
# --- エージェント(思考する人)クラス ---
class SmartAgent:
def __init__(self, id):
self.id = id
self.pos = np.array([random.uniform(0, 5), random.uniform(0, HEIGHT)])
self.vel = np.array([0.0, 0.0])
self.radius = 0.3
self.max_speed = 1.3 + random.uniform(-0.2, 0.2)
# 思考用パラメータ
self.decision_interval = random.randint(5, 15)
self.patience_factor = random.uniform(2.0, 4.0)
self.target_gate_idx = 0
self.color = np.random.rand(3,)
def get_gate_cost(self, gate_idx, agents):
gate_y = GATE_POSITIONS[gate_idx]
gate_pos = np.array([GATE_X, gate_y])
dist = np.linalg.norm(gate_pos - self.pos)
queue_count = 0
for other in agents:
if other.id != self.id:
if getattr(other, 'target_gate_idx', -1) == gate_idx:
if GATE_X - 5.0 < other.pos[0] < GATE_X:
if other.pos[0] > self.pos[0]:
queue_count += 1
return dist + (queue_count * self.patience_factor)
def think_best_gate(self, agents):
costs = [self.get_gate_cost(i, agents) for i in range(len(GATE_POSITIONS))]
return np.argmin(costs)
def update(self, step_count, agents, walls):
# リターゲティング処理
if self.pos[0] < GATE_X - 0.5:
if step_count % self.decision_interval == 0:
self.target_gate_idx = self.think_best_gate(agents)
# 目的地設定(ウェイポイント含む)
gate_y = GATE_POSITIONS[self.target_gate_idx]
if self.pos[0] < GATE_X - 1.5:
target_pos = np.array([GATE_X - 1.0, gate_y])
speed_limit = self.max_speed
elif self.pos[0] < GATE_X + WALL_THICKNESS:
target_pos = np.array([GATE_X + 2.0, gate_y])
if GATE_X - 0.5 < self.pos[0] < GATE_X + 0.5:
# ゲート通過時の減速
speed_limit = 0.6 if abs(self.pos[1] - gate_y) < GATE_WIDTH else 0.3
else:
speed_limit = self.max_speed
else:
target_pos = np.array([WIDTH + 2, self.pos[1]])
speed_limit = self.max_speed
# 物理演算(移動と衝突回避)
direction = target_pos - self.pos
if np.linalg.norm(direction) > 0: direction /= np.linalg.norm(direction)
desired_vel = direction * speed_limit
force = (desired_vel - self.vel) / 0.5
for other in agents:
if other.id != self.id:
diff = self.pos - other.pos
dist = np.linalg.norm(diff)
safe_dist = self.radius + other.radius + 0.1
if dist < safe_dist:
force += (diff / dist) * 2000.0 * np.exp(-(dist / 0.5))
for wall in walls:
# 壁の当たり判定(簡易版)
wx_min, wx_max = wall['x']
wy_min, wy_max = wall['y']
closest_pt = np.array([
max(wx_min, min(self.pos[0], wx_max)),
max(wy_min, min(self.pos[1], wy_max))
])
diff = self.pos - closest_pt
dist = np.linalg.norm(diff)
if dist < self.radius + 0.2:
if dist > 0:
force += (diff / dist) * 100.0 * (self.radius + 0.2 - dist)
# ウォールスライディング
normal = diff / dist
tangent = np.array([-normal[1], normal[0]])
force += tangent * np.dot(self.vel, tangent) * 5.0
else:
force += np.array([-1.0, 0]) * 200
force += np.random.normal(0, 2.0, 2)
self.vel += force * DT
speed = np.linalg.norm(self.vel)
if speed > speed_limit: self.vel = (self.vel / speed) * speed_limit
self.pos += self.vel * DT
# --- メイン処理と可視化 ---
walls = []
walls.append({'x': [-1, WIDTH+1], 'y': [-1, 0]})
walls.append({'x': [-1, WIDTH+1], 'y': [HEIGHT, HEIGHT+1]})
prev_y = 0
for gy in GATE_POSITIONS:
lower_y = gy - GATE_WIDTH / 2
walls.append({'x': [GATE_X, GATE_X + WALL_THICKNESS], 'y': [prev_y, lower_y]})
prev_y = gy + GATE_WIDTH / 2
walls.append({'x': [GATE_X, GATE_X + WALL_THICKNESS], 'y': [prev_y, HEIGHT]})
agents = [SmartAgent(i) for i in range(NUM_AGENTS)]
# 初回のターゲット決定
for agent in agents:
agent.target_gate_idx = agent.think_best_gate(agents)
history = []
print("AIシミュレーション計算中...")
for t in tqdm(range(SIM_DURATION), desc="Step"):
frame_pos = []
frame_colors = []
for agent in agents:
agent.update(t, agents, walls)
frame_pos.append(agent.pos.copy())
# ターゲットゲートに応じて色分け (0:赤, 1:緑, 2:青)
if agent.target_gate_idx == 0: c = [1, 0, 0]
elif agent.target_gate_idx == 1: c = [0, 1, 0]
else: c = [0, 0, 1]
frame_colors.append(c)
history.append((frame_pos, frame_colors))
# アニメーション作成
fig, ax = plt.subplots(figsize=(10, 5))
ax.set_xlim(0, WIDTH); ax.set_ylim(0, HEIGHT)
ax.set_title("【思考型】混雑を見て空いている列を選ぶ群衆")
for wall in walls:
rect = Rectangle((wall['x'][0], wall['y'][0]), wall['x'][1]-wall['x'][0], wall['y'][1]-wall['y'][0], color='gray')
ax.add_patch(rect)
for gy in GATE_POSITIONS: ax.plot([GATE_X, GATE_X+0.5], [gy, gy], 'k-')
scat = ax.scatter([], [], c=[], s=50, edgecolor='black')
def animate(i):
positions, colors = history[i]
scat.set_offsets(positions)
scat.set_color(colors)
ax.set_title(f"Time: {i*DT:.1f} s")
return scat,
ani = animation.FuncAnimation(fig, animate, frames=len(history), interval=30, blit=True)
ani.save("simulation_smart.mp4", writer="ffmpeg", fps=30)
print("動画保存完了")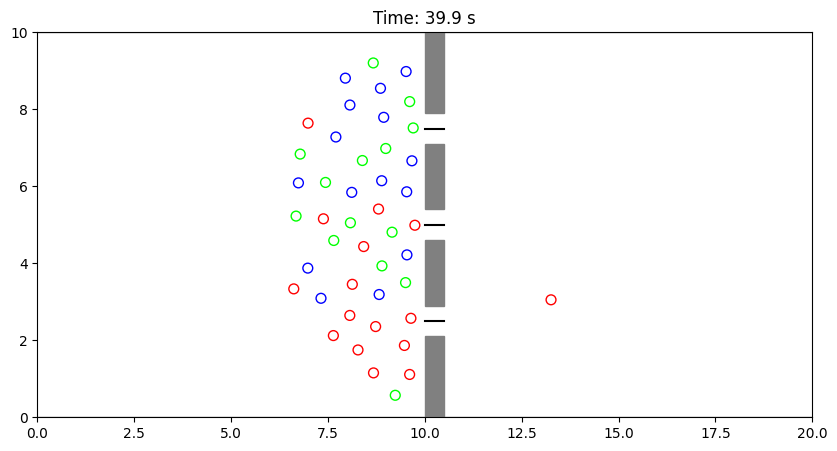
考察:個の最適化が導く全体の最適化
シミュレーションを実行して動画を見てみると、非常に興味深い現象が観察できます。
最初は一番上のゲート(赤)を目指していたエージェントが、改札の手前で混雑に気づき、すっと中央のゲート(緑)へ進路を変える様子が見られます。
結果として、3つのゲートには均等に人が流れ込み、「空いているゲートがあるのに誰も使わない」という非効率な状態が解消されています。
これは経済学やゲーム理論でいうパレート改善(Pareto Improvement)に近い現象です。各エージェントは「自分ができるだけ早く通過したい」という利己的な理由で行動していますが、その結果として混雑が分散され、システム全体のスループット(時間当たりの処理人数)が向上しています。
システム側(駅員など)が「空いている方へお進みください」と強制しなくても、個々のエージェントに適切な情報(混雑状況)と判断基準(コスト関数)を与えるだけで、全体最適が達成されるのです。これを自律分散型システムの強みと言えます。
まとめ
今回は、マルチエージェントシミュレーションに「知覚」と「判断」のロジックを組み込むことで、動的にターゲットを変更し、負荷分散を行う方法を解説しました。
- コスト関数: 距離と待ち時間を天秤にかける判断基準。
- 知覚: 自分より前にいる人数を数える簡易的なセンシング。
- 非同期決定: 判断タイミングをずらすことで集団の振動を防ぐ。
これらを実装することで、単なる物理粒子のシミュレーションから、意思を持った群衆のシミュレーションへと進化させることができました。
今回はルールベース(ヒューリスティック)で思考を記述しましたが、これをさらに発展させて、強化学習(Reinforcement Learning)を用いて「試行錯誤の中から最適なコスト感覚を学習させる」といったアプローチも可能です。PyTorchなどのフレームワークを使えば、より複雑で予測不能な環境にも適応できるAIエージェントを作ることができるでしょう。
ぜひ、パラメータ(patience_factorなど)を変えて実験し、群衆の性格が変わると流れがどう変わるか観察してみてください。それでは、また次回の記事でお会いしましょう!
今回も最後まで読んでいただきありがとうございました。



コメント