Pythonで学ぶ数値計算のアルゴリズムと実装第1回：多項式計算とテイラー展開

こんにちは、JS2IIUです。
今回から始まるこの連載では、プログラミング言語Python、そして機械学習のデファクトスタンダードであるPyTorchを活用しながら、数値計算の根幹をなすアルゴリズムを学んでいきます。

機械学習やAIのモデルを扱う際、私たちはしばしば「ブラックボックス」として関数を利用しがちです。しかし、その内部でどのように数値が処理され、複雑な数式がどのようにコンピュータが扱える形に変換されているのかを知ることは、アルゴリズムの効率化や誤差の制御、さらには新しいAIモデルの設計において非常に大きな武器となります。

第1回目となる今回は、あらゆる数値計算の基礎となる「多項式計算」の効率化と、複雑な関数を多項式へと変換する「テイラー展開」に焦点を当てます。今回もよろしくお願いします。

1. 多項式の計算と「ホーナー法」の重要性
1. ホーナー法のアルゴリズム
  1. ビッグオー記法
2. Pythonによる実装
2. 複雑な関数を近似する：テイラー展開
1. 近似精度の考え方
3. テイラー展開の実装と視覚化
1. コードの解説
2. 実行結果の考察
4. 数値的安定性
1. 例：Softmaxの数値安定化
まとめ
連載記事、各回へのリンク

1. 多項式の計算と「ホーナー法」の重要性

まず、最も基本的な関数である多項式を考えてみましょう。多項式は以下のような形で表されます。

$$P(x) = a_n x^n + a_{n-1} x^{n-1} + \dots + a_1 x + a_0$$

この式を愚直にプログラムで計算しようとすると、各項ごとに $x$ のべき乗を計算し、それに係数を掛けるという手順を踏むことになります。しかし、$x^k$ を計算するために「$x$ を $k$ 回掛ける」という処理を行うと、多項式の次数 $n$ が大きくなるにつれて、掛け算の回数が指数関数的に増えてしまいます。

数値計算において、計算コスト（時間）と精度（丸め誤差の蓄積）は常にトレードオフの関係にあります。そこで登場するのが「ホーナー法（Horner’s Method）」です。

ホーナー法のアルゴリズム

ホーナー法（Horner’s Method）は、多項式の計算を効率化するための古典的かつ非常に重要なアルゴリズムです。多項式

$$P(x) = a_n x^n + a_{n-1} x^{n-1} + \dots + a_1 x + a_0$$

をそのまま計算しようとすると、各項ごとに $x$ のべき乗を計算し、係数を掛けて足し合わせる必要があります。これは指数関数的に計算コストが増大し、特に高次多項式では非効率的です。

ホーナー法では、多項式を次のように入れ子（ネスト）状に変形します：

$$P(x) = (\dots((a_n x + a_{n-1})x + a_{n-2})x + \dots + a_1)x + a_0$$

この変形の本質は、べき乗の計算を繰り返しの掛け算に置き換え、計算途中の値を逐次的に更新していく点にあります。これにより、

掛け算の回数が $n$ 回、足し算も $n$ 回 で済みます（$n$ は多項式の次数）。
べき乗の計算や中間結果の再利用が不要となり、計算量は $O(n)$ となります。
メモリ効率も高く、逐次的な計算のため数値的な安定性も向上します。

また、ホーナー法は浮動小数点演算における丸め誤差の蓄積を抑える効果もあり、科学技術計算や機械学習の現場でも広く利用されています。特に、GPUやSIMD命令による並列計算との相性も良く、PyTorchやNumPyなどの数値計算ライブラリでも内部的に利用されることが多いです。

このように、ホーナー法は「計算量の削減」「数値安定性」「実装の簡潔さ」という観点から、実用的な多項式評価アルゴリズムのデファクトスタンダードとなっています。

ビッグオー記法

ビッグオー記法は、アルゴリズムの実行時間やメモリ使用量が入力サイズ $n$ に対してどのように増加するかを簡潔に表現するための記法です。詳細はこちらの記事を参考にして下さい。

Pythonによる実装

それでは、PyTorchを用いてホーナー法を実装してみましょう。AIエンジニアにとって馴染み深いPyTorchのTensor型を使用することで、将来的にGPUアクセラレーションを考慮した計算にも対応できます。

Python

import torch

def evaluate_polynomial_horner(coefficients, x):
    """
    ホーナー法を用いて多項式の値を計算する関数

    Args:
        coefficients (torch.Tensor): 多項式の係数 [a_n, a_{n-1}, ..., a_0] の順
        x (float or torch.Tensor): 変数 x の値

    Returns:
        torch.Tensor: 計算結果 P(x)
    """
    # 係数のリストから最高次の係数を取り出し、初期値とする
    result = torch.zeros_like(torch.tensor(x)) + coefficients[0]

    # 残りの係数に対して、result = result * x + coefficient を繰り返す
    # coefficients[1:] をループで回す
    for i in range(1, len(coefficients)):
        result = result * x + coefficients[i]

    return result

# テスト例: P(x) = 2x^3 - 6x^2 + 2x - 1 を x = 3 で計算
# 係数は [2, -6, 2, -1]
coeffs = torch.tensor([2.0, -6.0, 2.0, -1.0])
x_val = 3.0

output = evaluate_polynomial_horner(coeffs, x_val)
print(f"P({x_val}) = {output.item()}") # 期待値: 2*(27) - 6*(9) + 2*(3) - 1 = 54 - 54 + 6 - 1 = 5

import torch

def evaluate_polynomial_horner(coefficients, x):
    """
    ホーナー法を用いて多項式の値を計算する関数

    Args:
        coefficients (torch.Tensor): 多項式の係数 [a_n, a_{n-1}, ..., a_0] の順
        x (float or torch.Tensor): 変数 x の値

    Returns:
        torch.Tensor: 計算結果 P(x)
    """
    # 係数のリストから最高次の係数を取り出し、初期値とする
    result = torch.zeros_like(torch.tensor(x)) + coefficients[0]

    # 残りの係数に対して、result = result * x + coefficient を繰り返す
    # coefficients[1:] をループで回す
    for i in range(1, len(coefficients)):
        result = result * x + coefficients[i]

    return result

# テスト例: P(x) = 2x^3 - 6x^2 + 2x - 1 を x = 3 で計算
# 係数は [2, -6, 2, -1]
coeffs = torch.tensor([2.0, -6.0, 2.0, -1.0])
x_val = 3.0

output = evaluate_polynomial_horner(coeffs, x_val)
print(f"P({x_val}) = {output.item()}") # 期待値: 2*(27) - 6*(9) + 2*(3) - 1 = 54 - 54 + 6 - 1 = 5

このコードでは、for ループの中で、一つ前の計算結果に $x$ を掛けて次の係数を足すという操作を繰り返しています。非常にシンプルですが、これが最も効率的で数値的に安定した多項式の評価方法です。

2. 複雑な関数を近似する：テイラー展開

数値計算において、私たちはしばしば $\sin(x)$、$\cos(x)$、$\exp(x)$、$\log(x)$ といった「超越関数」を扱います。しかし、コンピュータは基本的に加減乗除といった四則演算しか実行できません。では、どのようにして $\sin(x)$ の値を求めているのでしょうか。

その答えの一つが「テイラー展開（Taylor Expansion）」です。テイラー展開とは、ある一点の周りで関数を無限次の多項式として表現する手法です。

関数 $f(x)$ が点 $a$ において無限回微分可能であるとき、テイラー展開は以下のように表されます。

$$f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!}(x-a)^n$$

特に $a=0$ の場合を「マクローリン展開」と呼びます。実用上、この無限和を途中の第 $N$ 項で打ち切ることで、元の関数を $N$ 次の多項式として「近似」します。

近似精度の考え方

第 $N$ 項までの近似を用いた場合、残りの項は「剰余項」と呼ばれ、これが近似誤差となります。一般に、展開の中心点 $a$ から遠ざかるほど誤差は大きくなり、次数 $N$ を増やすほど近似精度は向上します。

3. テイラー展開の実装と視覚化

今回は、代表的な例として $\sin(x)$ 関数のマクローリン展開を実装してみます。$\sin(x)$ のマクローリン展開は以下の通りです。

$$\sin(x) \approx x – \frac{x^3}{3!} + \frac{x^5}{5!} – \frac{x^7}{7!} + \dots$$

この近似がどれほど正確なのか、次数を増やしながら視覚的に確認してみましょう。ここでは「自動微分」ライブラリを使わずに、テイラー展開の定義に基づいて係数を直接計算するコードを作成します。

Python

import torch
import matplotlib.pyplot as plt
import math

def sin_taylor_coefficients(n_terms):
    """
    sin(x)のマクローリン展開の係数を生成する
    x^0, x^1, x^2, ..., x^n までの係数をリストで返す
    """
    coeffs = []
    for i in range(n_terms + 1):
        if i % 2 == 0:
            coeffs.append(0.0) # 偶数次は0
        else:
            # sinのn次導関数から係数を決定
            # 1次: 1, 3次: -1, 5次: 1, ...
            sign = 1 if (i // 2) % 2 == 0 else -1
            coeffs.append(sign / math.factorial(i))

    # 高次から低次の順（ホーナー法用）に反転させる
    coeffs.reverse()
    return torch.tensor(coeffs)

# グラフ描画用の設定
x = torch.linspace(-10, 10, 500)
y_true = torch.sin(x)

plt.figure(figsize=(10, 6))
plt.plot(x.numpy(), y_true.numpy(), label='True sin(x)', color='black', lw=2)

# 次数を変えて近似をプロット
orders = [3, 5, 7, 11]
for n in orders:
    coeffs = sin_taylor_coefficients(n)
    # 前回作成したホーナー法関数を使用して計算
    y_approx = evaluate_polynomial_horner(coeffs, x)

    plt.plot(x.numpy(), y_approx.numpy(), label=f'Taylor Order {n}')

plt.ylim(-2, 2)
plt.title('Approximation of sin(x) via Taylor Expansion')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.legend()
plt.grid(True)
plt.show()

import torch
import matplotlib.pyplot as plt
import math

def sin_taylor_coefficients(n_terms):
    """
    sin(x)のマクローリン展開の係数を生成する
    x^0, x^1, x^2, ..., x^n までの係数をリストで返す
    """
    coeffs = []
    for i in range(n_terms + 1):
        if i % 2 == 0:
            coeffs.append(0.0) # 偶数次は0
        else:
            # sinのn次導関数から係数を決定
            # 1次: 1, 3次: -1, 5次: 1, ...
            sign = 1 if (i // 2) % 2 == 0 else -1
            coeffs.append(sign / math.factorial(i))

    # 高次から低次の順（ホーナー法用）に反転させる
    coeffs.reverse()
    return torch.tensor(coeffs)

# グラフ描画用の設定
x = torch.linspace(-10, 10, 500)
y_true = torch.sin(x)

plt.figure(figsize=(10, 6))
plt.plot(x.numpy(), y_true.numpy(), label='True sin(x)', color='black', lw=2)

# 次数を変えて近似をプロット
orders = [3, 5, 7, 11]
for n in orders:
    coeffs = sin_taylor_coefficients(n)
    # 前回作成したホーナー法関数を使用して計算
    y_approx = evaluate_polynomial_horner(coeffs, x)

    plt.plot(x.numpy(), y_approx.numpy(), label=f'Taylor Order {n}')

plt.ylim(-2, 2)
plt.title('Approximation of sin(x) via Taylor Expansion')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.legend()
plt.grid(True)
plt.show()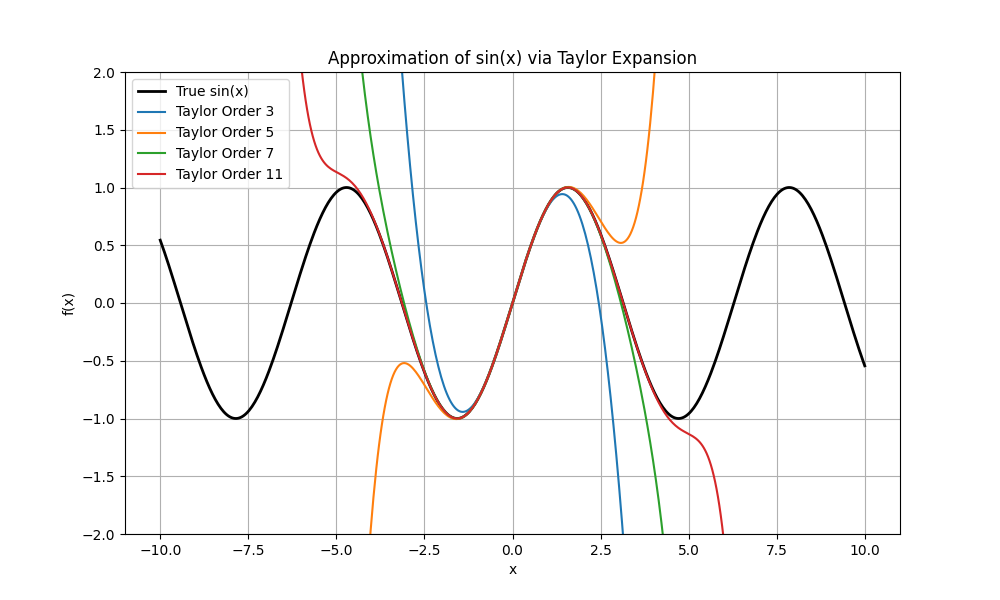

コードの解説

sin_taylor_coefficients: $\sin(x)$ の各項の係数を計算しています。$\sin(x)$ は奇関数なので、偶数次の係数はすべて $0$ になります。また、符号が交互に反転する性質を実装しています。
evaluate_polynomial_horner: 第1節で作成した関数を再利用しています。テイラー展開の結果得られた係数を多項式として効率的に計算します。
matplotlib による描画: 真の $\sin(x)$ と、3次、5次、7次、11次の近似多項式を比較しています。

実行結果の考察

グラフを見ると、展開の中心点である $x=0$ 付近では低い次数でも非常に正確に近似できていることがわかります。しかし、中心から離れる（$x$ の絶対値が大きくなる）につれて、急激に精度が悪化し、真の関数から乖離していきます。

これは数値計算における重要な教訓を与えてくれます。
「どんなに優れた近似式も、有効な範囲（収束半径）が存在する」ということです。

4. 数値的安定性

数値計算における「数値的安定性」とは、計算過程で発生する丸め誤差やオーバーフロー・アンダーフローなどの問題を最小限に抑え、信頼できる結果を得るための性質や工夫を指します。

テイラー展開の実装例では、math.factorial(i)（階乗）を用いて係数を計算しますが、次数 $n$ が大きくなると階乗の値は指数関数的に増大し、64ビット浮動小数点数でもすぐに表現限界（オーバーフロー）に達します。また、$x^n$ の計算も同様に急激に大きな値や小さな値となり、丸め誤差やアンダーフローの原因となります。

このような問題を回避するため、実際の数値計算ライブラリ（例：math.sin や torch.sin）では、以下のような高度なテクニックが組み合わされています：

レンジ・リダクション（range reduction）：入力 $x$ を $[-\pi, \pi]$ や $[0, 2\pi]$ などの狭い範囲に正規化し、テイラー展開の収束性と精度を高める。
分割計算や多重精度演算：高次の項を直接計算せず、分割統治的に計算したり、多重精度型（例えばfloat128や任意精度演算）を利用する。
数値安定な再帰的アルゴリズム：ホーナー法のように、逐次的な計算で丸め誤差の伝播を抑える。
近似式の切り替え：入力値の大きさや用途に応じて、テイラー展開以外の近似式（パデ近似、チェビシェフ多項式など）を自動的に選択する。

また、AIエンジニアがニューラルネットワークや統計モデルを実装する際にも、数値的安定性は極めて重要です。例えば、Softmax関数の計算では、指数関数のオーバーフローを防ぐために「最大値を引いてからexpを計算する」工夫が定番です。

例：Softmaxの数値安定化

$$
\mathrm{Softmax}(x_i) = \frac{\exp(x_i – \max_j x_j)}{\sum_j \exp(x_j – \max_k x_k)}
$$

このような工夫を怠ると、学習が発散したり、NaN（非数）やInf（無限大）が発生してしまうため、実装時には必ず「数値的安定性」を意識することが求められます。

まとめ

今回は「Pythonを使った数値計算」の連載第1回として、以下の内容を学びました。

多項式計算の効率化: ホーナー法を用いることで、計算量を $O(n)$ に抑え、数値的な安定性を向上させることができる。
関数の近似: テイラー展開を利用すれば、複雑な関数をコンピュータが得意な多項式に変換できる。
近似の限界: 次数を上げるほど精度は向上するが、中心点から離れると誤差が拡大するため、利用範囲に注意が必要である。

数値計算は、一見すると地味な分野に思えるかもしれません。しかし、ディープラーニングの勾配計算や最適化アルゴリズムの背後には、常にこうした「関数の評価」と「近似」の技術が息づいています。

次回は、今回学んだ多項式の知識を応用し、点と点の間を埋める「多項式補間」と「チェビシェフ補間」について解説します。データ解析において非常に重要なテーマですので、ぜひお楽しみに。

最後まで読んでいただきありがとうございます。

連載記事、各回へのリンク

Pythonで学ぶ数値計算のアルゴリズムと実装第1回：多項式計算とテイラー展開 | アマチュア無線局JS2IIU
https://js2iiu.com/2025/12/31/python_numerical_01/

Pythonで学ぶ数値計算のアルゴリズムと実装第2回：多項式補間とチェビシェフ補間の戦略 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/01/python_numerical_02/

Pythonで学ぶ数値計算のアルゴリズムと実装第3回：積分の基礎：中点則、台形則からシンプソン則まで | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/01/python_numerical_03/

Pythonで学ぶ数値計算のアルゴリズムと実装第4回：高度な数値積分：二重指数型（DE）公式と広義積分 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/01/python_numerical_04/

Pythonで学ぶ数値計算のアルゴリズムと実装第5回：計算の「正しさ」を評価する：ノルムと条件数 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/01/python_numeric_05/

Pythonで学ぶ数値計算のアルゴリズムと実装第6回：連立一次方程式の直截解法：ガウス消去法とピボット選択 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/01/python_numerical_06/

Pythonで学ぶ数値計算のアルゴリズムと実装第8回：スパース性を活かす：帯行列の高速計算アルゴリズム | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/02/python_numerical_08/

Pythonで学ぶ数値計算のアルゴリズムと実装第9回：最小二乗法とQR分解：ハウスホルダー変換による安定化 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/02/python_numerial_09/

Pythonで学ぶ数値計算のアルゴリズムと実装第10回：非線形方程式の探索：2分法からニュートン法まで | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/03/python_numerical_10/

Pythonで学ぶ数値計算のアルゴリズムと実装第11回：行列の本質を捉える：固有値問題の数値解法 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/03/python_numerical_11/

Pythonで学ぶ数値計算のアルゴリズムと実装第12回：現象の変化を追う：ルンゲ・クッタ法による常微分方程式の解法 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/03/python_numerical_12/

Pythonで学ぶ数値計算のアルゴリズムと実装第13回：空間の熱と振動を解く：偏微分方程式の差分近似と反復解法 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/03/python_numerical_13/

月	火	水	木	金	土	日
1	2	3	4	5	6	7
8	9	10	11	12	13	14
15	16	17	18	19	20	21
22	23	24	25	26	27	28
29	30	31