こんにちは、JS2IIUです。
数値計算連載の第9回となる今回は、機械学習や統計学のバックボーンとも言える「最小二乗法」を取り上げます。
私たちはこれまで、連立一次方程式 \(Ax = b\) を解く方法を学んできました。しかし、現実のデータ分析では、未知数の数よりも観測データの数の方が圧倒的に多い、いわゆる「過剰条件」の状態が一般的です。この場合、すべての式を完璧に満たす解 \(x\) は存在しません。そこで、「誤差の二乗和を最小にする」という戦略をとる最小二乗法が登場します。
今回は、理論上は正しいものの数値的に不安定な「正規方程式」の問題点を指摘し、現代の数値計算において標準的に使われる「ハウスホルダー変換によるQR分解」を用いた、極めて安定な解法を実装していきます。今回もよろしくお願いします。
1. はじめに:解けない方程式をどう扱うか
現実のデータ解析や機械学習の現場では、観測データの数(\(m\))が推定したいパラメータの数(\(n\))よりも多い、いわゆる「過剰条件」の状況が一般的です。例えば、直線や曲線をデータにフィットさせたい場合、観測点は数十点、数百点とある一方で、直線なら2つ、2次曲線なら3つと、パラメータの数はごくわずかです。
このとき、\(Ax = b\) という形の連立一次方程式を考えると、\(A\) は縦長(\(m > n\))の行列となり、すべての式を同時に満たす \(x\) は通常存在しません。なぜなら、実際のデータには必ずノイズや誤差が含まれており、全ての観測点を一本の直線や曲線が完璧に通ることは現実的に不可能だからです。
このような「解けない方程式」をどう扱うか?ここで登場するのが「最小二乗法」です。すべての式を厳密に満たすのではなく、
「なるべく全体として誤差が小さくなる」\(x\) を探す、という発想に切り替えます。
具体的には、\(Ax\) で表されるモデルの出力と、実際の観測値 \(b\) との差(残差)\(r = b – Ax\) を考え、その大きさ(L2ノルムの二乗)\(|r|^2\) を最小にする \(x\) を求めます。これは「全観測点に対する誤差の合計が最も小さくなるようなパラメータ」を意味し、ディープラーニングにおける「損失関数の最小化」の最も基本的な形でもあります。
このアプローチにより、現実のデータのばらつきやノイズを考慮しつつ、最も「妥当な」解を見つけることができるのです。
2. 正規方程式とその不安定性
最小二乗法の解を求める最も基本的な方法は、「正規方程式(Normal Equations)」を解くことです。これは、最小二乗誤差 \(|b – Ax|^2\) を \(x\) について最小化するために、\(x\) で微分して0とおくことで導かれます。
$$A^T A x = A^T b$$
ここで、
- \(A\):観測データから作られる \(m \times n\) 行列(\(m > n\))
- \(x\):求めたいパラメータ(\(n\) 次元ベクトル)
- \(b\):観測値(\(m\) 次元ベクトル)
- \(A^T\):\(A\) の転置行列
この正規方程式は、\(A^T A\) という \(n \times n\) の正方行列を係数とする連立一次方程式です。\(A^T A\) は「グラム行列」とも呼ばれ、\(A\) の列ベクトル同士の内積から構成されます。
この連立方程式は、通常の線形方程式の解法(例えば第7回で紹介したコレスキー分解やガウス消去法など)で解くことができます。
しかし、ここに大きな数値的落とし穴があります。
条件数とは?
「条件数」とは、行列の“数値的な安定性”や“逆行列を計算したときの誤差の増幅度”を表す指標です。条件数が大きい(例えば \(10^4\) やそれ以上)と、計算機上での丸め誤差やデータのノイズが解に大きく影響し、信頼できない結果になることがあります。
\(A\) の条件数を \(\kappa\) とすると、正規方程式の係数行列 \(A^T A\) の条件数は \(\kappa^2\) となります。つまり、元の行列よりも“二乗”も悪化してしまうのです。
例:
もし \(A\) の条件数が \(10^4\) なら、\(A^T A\) の条件数は \(10^8\) となり、計算結果の信頼性が大きく損なわれます。
このような理由から、正規方程式は理論的には正しいものの、実際の数値計算では不安定になりやすいという重大な欠点があります。
この問題を回避するためには、「行列を二乗しない」=「\(A^T A\) を作らない」方法、すなわちQR分解などの直交変換を使ったアプローチが重要となります。
3. QR分解:直交行列による安定化
正規方程式の数値的不安定性を克服するために、現代の数値計算で広く使われているのが「QR分解」です。
QR分解とは、任意の \(m \times n\) 行列 \(A\) を、
$$A = QR$$
という形に分解する手法です。
- \(Q\): \(m \times m\) の直交行列(\(Q^T Q = I\))。直交行列とは、列ベクトル同士がすべて直交し、かつ長さが1であるような行列です。直交行列をかけてもベクトルの長さや角度は変わりません(回転や鏡映のみ)。
- \(R\): \(m \times n\) の上三角行列。上三角行列とは、対角成分より下がすべて0の行列です。
この分解の直感的な意味は、「複雑な変換(\(A\))を、“回転(\(Q\))”と“伸縮・合成(\(R\))”に分けて考える」ことです。
なぜQR分解で安定するのか?
QR分解を使うと、最小二乗問題は次のように変形できます:
$$Ax = b \implies QRx = b \implies Rx = Q^T b$$
ここで、\(Q\) は直交行列なので、逆行列を求める必要はなく、単に転置(\(Q^T\))をかけるだけでOKです。直交行列は「条件数を変化させない」「誤差を増幅しない」という非常に優れた性質を持っています。
また、\(R\) は上三角行列なので、未知数 \(x\) を後退代入(back substitution)で効率よく求めることができます。
このように、QR分解を用いることで、
- 行列の条件数の悪化を防ぎ、
- 数値的に安定したまま最小二乗解を得ることができる
という大きなメリットがあります。
このため、実務や科学技術計算の現場では「正規方程式ではなくQR分解を使う」ことが標準となっています。
4. ハウスホルダー変換の理論と直感的理解
QR分解を効率的かつ安定に行うための代表的なアルゴリズムが「ハウスホルダー変換(Householder Transformation)」です。
ハウスホルダー変換とは?
ハウスホルダー変換は、あるベクトルを特定の超平面(鏡)に対して“鏡映”する(反射させる)操作です。数式で表すと、任意の単位ベクトル \(v\) に対して、
$$
H = I – 2vv^T
$$
という形の行列 \(H\) を「ハウスホルダー行列」と呼びます。\(H\) は直交行列かつ対称行列であり、\(H^T = H\), \(H^2 = I\) という性質を持ちます。
\(H\) をベクトル \(x\) に作用させると、\(x\) を \(v\) を法線とする超平面で鏡映したベクトルが得られます。
QR分解への応用
QR分解では、行列 \(A\) の各列について、対角成分より下の要素を一気に0にするようなハウスホルダー行列 \(H_k\) を順番に構成します。
例えば、\(A\) の第1列 \(a_1\) について、
- \(a_1\) の下半分を0にしたい → \(a_1\) を \(e_1\)(最初の単位ベクトル)方向に揃えるような鏡映を作る
- \(v = a_1 + \text{sign}(a_{11}) |a_1| e_1\) とし、\(v\) を正規化
- \(H_1 = I – 2vv^T\) を作り、\(A\) の左から掛ける
これを各列ごとに繰り返すことで、\(A\) は上三角行列 \(R\) へと変換されていきます。
\(Q\) は、すべてのハウスホルダー行列の積(\(Q = H_1 H_2 … H_n\))として得られます。
幾何学的な直感
ハウスホルダー変換は「鏡」を使ってベクトルを軸上に整列させる操作です。1回の変換で列全体の下半分を一気に0にできるため、ギブンス回転(1要素ずつ消す)よりも大規模行列で効率的です。
- ハウスホルダー変換は、直交行列による鏡映操作であり、数値的に安定
- QR分解の標準的な実装手法であり、特に大きな行列で威力を発揮
- 数式:\(H = I – 2vv^T\) を繰り返し適用し、\(A\) を上三角化
5. PyTorchによるハウスホルダーQR分解の実装
それでは、PyTorchを用いてハウスホルダーQR分解を実装してみましょう。PyTorchのテンソル操作を活用することで、ループを最小限に抑えた実装が可能です。
import torch
def householder_qr(A):
"""
ハウスホルダー変換を用いて行列 A を QR 分解する
Args:
A (torch.Tensor): m x n の行列
Returns:
Q (torch.Tensor): m x m の直交行列
R (torch.Tensor): m x n の上三角行列
"""
m, n = A.shape
R = A.clone().float()
Q = torch.eye(m, device=A.device, dtype=A.dtype)
# 列ごとに処理して下半分を0にしていく
for k in range(n):
# 現在の列の、対角成分以下のベクトルを取り出す
x = R[k:, k]
# ハウスホルダーベクトルの作成
e1 = torch.zeros_like(x)
e1[0] = 1.0
# 数値的安定性のために符号を選択
sign = 1.0 if x[0] >= 0 else -1.0
v = x + sign * torch.norm(x) * e1
v = v / torch.norm(v) # 正規化
# Rに行列 H = I - 2vv^T を左から掛ける操作
# 直接行列を作らずにベクトル演算で適用 (R = R - 2v(v^T R))
R[k:, k:] -= 2.0 * torch.outer(v, torch.matmul(v, R[k:, k:]))
# Qに行列 H を右から掛ける操作 (Q = Q H)
# Q = Q - 2(Qv)v^T
Q[:, k:] -= 2.0 * torch.outer(torch.matmul(Q[:, k:], v), v)
return Q, R
# テスト
A_sample = torch.tensor([[1.0, 2.0], [3.0, 4.0], [5.0, 6.0]])
Q, R = householder_qr(A_sample)
print("Matrix Q (Orthogonal):\n", Q)
print("Matrix R (Upper Triangular):\n", R)
print("\nVerification (Q @ R):\n", torch.matmul(Q, R))Matrix Q (Orthogonal):
tensor([[-0.1690, 0.8971, 0.4082],
[-0.5071, 0.2760, -0.8165],
[-0.8452, -0.3450, 0.4082]])
Matrix R (Upper Triangular):
tensor([[-5.9161e+00, -7.4374e+00],
[-2.3842e-07, 8.2808e-01],
[ 0.0000e+00, -1.1921e-07]])
Verification (Q @ R):
tensor([[1.0000, 2.0000],
[3.0000, 4.0000],
[5.0000, 6.0000]])コードの解説
- 数値的安定性:
signの選択は、ベクトル \(x\) と \(e_1\) が打ち消し合って非常に小さな値になる(桁落ち)のを防ぐための工夫です。 - outer演算: ハウスホルダー行列 \(H = I – 2vv^T\) を明示的に作ると \(O(m^2)\) のメモリが必要になりますが、
outer(外積)とmatmul(内積)を組み合わせることで、メモリを節約しつつ高速に計算しています。 - 直交性の維持: この手法で得られる \(Q\) は、浮動小数点の精度の範囲内で極めて正確に直交性を維持します。
8. 実践:最小二乗法による関数の推定
求めたQR分解を使って、最小二乗問題を解いてみましょう。
具体的には、ノイズの乗ったデータに対して「多項式曲線」をフィットさせます。
def solve_least_squares_qr(A, b):
"""
QR分解を用いて最小二乗解を求める (Rx = Q^T b)
"""
Q, R = householder_qr(A)
m, n = A.shape
# Q^T * b を計算
qty = torch.matmul(Q.t(), b.float())
# Rx = (Q^T b) の上部 n 行を解く (後退代入)
# R は m x n なので、上部の n x n 部分を使用
R_upper = R[:n, :n]
b_upper = qty[:n]
# 後退代入 (第6回で学んだ手法)
x = torch.linalg.solve_triangular(R_upper, b_upper.unsqueeze(1), upper=True)
return x.flatten()
# --- 実践:多項式フィッティング ---
# 真の関数: y = 0.5x^2 - 2x + 1
x_data = torch.linspace(-2, 4, 20)
y_true = 0.5 * x_data**2 - 2 * x_data + 1
y_noisy = y_true + torch.randn_like(x_data) * 0.5 # ノイズ追加
# Vandermonde行列 A の作成 (2次多項式を想定)
# A = [x^2, x^1, 1]
A_poly = torch.stack([x_data**2, x_data, torch.ones_like(x_data)], dim=1)
# QR分解で解を求める
params = solve_least_squares_qr(A_poly, y_noisy)
print("\nEstimated Parameters:", params)
# 可視化 (Matplotlib)
import matplotlib.pyplot as plt
plt.scatter(x_data, y_noisy, label="Noisy Data", color="red")
x_fine = torch.linspace(-2, 4, 100)
y_pred = params[0] * x_fine**2 + params[1] * x_fine + params[2]
plt.plot(x_fine, y_pred, label="Least Squares Fit (QR)", color="blue")
plt.legend()
plt.title("Polynomial Fitting via QR Decomposition")
plt.show()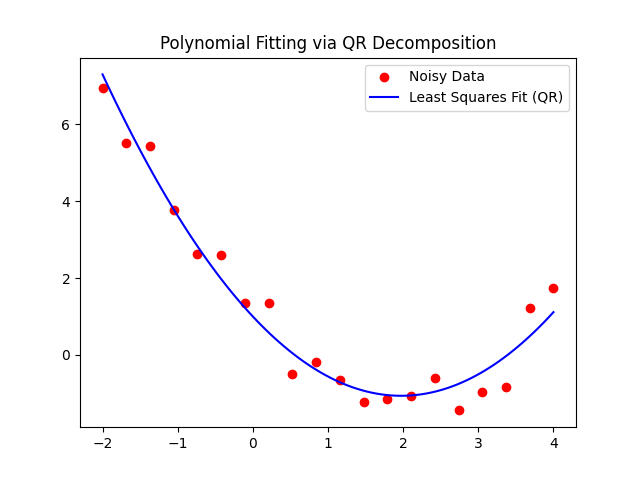
結果の考察
グラフを見ると、バラついたデータの間を縫うように、元の放物線に近い曲線が推定されていることがわかります。もしここで正規方程式を使っていた場合、多項式の次数が上がると(例えば10次など)、行列の条件数が急激に悪化し、曲線が不自然に波打つ現象が起きます。QR分解によるアプローチは、そうした不安定さに対して非常に堅牢です。
7. 実践的なアドバイス:ライブラリの使い分け
実務で最小二乗法を解く場合、PyTorchの torch.linalg.lstsq を使うのが最も効率的です。
# PyTorch標準の最小二乗ソルバー
# driver='gelsd' を指定すると、内部で特異値分解(SVD)が使われ、さらに安定します
solution = torch.linalg.lstsq(A_poly, y_noisy.unsqueeze(1))
params_torch = solution.solution.flatten()自作のQR分解は、アルゴリズムの挙動を深く理解し、特定の制約条件下でカスタマイズが必要な場合に役立ちます。また、ハウスホルダー変換そのものは、後で学ぶ固有値計算の「前処理」としても極めて重要です。
まとめ
第9回では、最小二乗法の数値的な安定性を支えるQR分解とハウスホルダー変換について学びました。
- 過剰条件な問題では、厳密な解の代わりに「誤差の最小化」を目指す。
- 正規方程式は実装が容易だが、条件数を悪化させるため数値的に不安定。
- QR分解は、行列を回転・鏡映させることで「大きさを変えずに」解きやすい形へ変形する。
- ハウスホルダー変換は、鏡映を利用して行列を一気に上三角化する、QR分解の標準的なアルゴリズム。
「正規方程式ではなくQR分解を使う」という選択ができるようになることは、数値計算に強いエンジニアへの大きな一歩です。
次回からは、これまでの「線形」の世界を飛び出し、曲線と曲線の交点などを探る「非線形方程式」の探索アルゴリズムについて解説します。ニュートン法などの有名な手法をPythonで解き明かしていきましょう。お楽しみに。
最後まで読んでいただきありがとうございます。
連載記事、各回へのリンク
Pythonで学ぶ数値計算のアルゴリズムと実装 第1回:多項式計算とテイラー展開 | アマチュア無線局JS2IIU
https://js2iiu.com/2025/12/31/python_numerical_01/
Pythonで学ぶ数値計算のアルゴリズムと実装 第2回:多項式補間とチェビシェフ補間の戦略 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/01/python_numerical_02/
Pythonで学ぶ数値計算のアルゴリズムと実装 第3回:積分の基礎:中点則、台形則からシンプソン則まで | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/01/python_numerical_03/
Pythonで学ぶ数値計算のアルゴリズムと実装 第4回:高度な数値積分:二重指数型(DE)公式と広義積分 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/01/python_numerical_04/
Pythonで学ぶ数値計算のアルゴリズムと実装 第5回:計算の「正しさ」を評価する:ノルムと条件数 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/01/python_numeric_05/
Pythonで学ぶ数値計算のアルゴリズムと実装 第6回:連立一次方程式の直截解法:ガウス消去法とピボット選択 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/01/python_numerical_06/
Pythonで学ぶ数値計算のアルゴリズムと実装 第8回:スパース性を活かす:帯行列の高速計算アルゴリズム | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/02/python_numerical_08/
Pythonで学ぶ数値計算のアルゴリズムと実装 第9回:最小二乗法とQR分解:ハウスホルダー変換による安定化 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/02/python_numerial_09/
Pythonで学ぶ数値計算のアルゴリズムと実装 第10回:非線形方程式の探索:2分法からニュートン法まで | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/03/python_numerical_10/
Pythonで学ぶ数値計算のアルゴリズムと実装 第11回:行列の本質を捉える:固有値問題の数値解法 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/03/python_numerical_11/
Pythonで学ぶ数値計算のアルゴリズムと実装 第12回:現象の変化を追う:ルンゲ・クッタ法による常微分方程式の解法 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/03/python_numerical_12/
Pythonで学ぶ数値計算のアルゴリズムと実装 第13回:空間の熱と振動を解く:偏微分方程式の差分近似と反復解法 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/03/python_numerical_13/



コメント