Pythonで学ぶ数値計算のアルゴリズムと実装 第10回：非線形方程式の探索：2分法からニュートン法まで

こんにちは、JS2IIUです。

数値計算連載の第10回目となる今回は、これまでの「線形（まっすぐ）」な世界から一歩踏み出し、より複雑な「非線形（曲がった）」な方程式を解くアルゴリズムを探求します。

これまでの回では \(Ax = b\) のような連立一次方程式を扱ってきましたが、現実の科学やエンジニアリング、そしてAIの最適化問題で私たちが直面するのは \(f(x) = 0\) という形の非線形方程式です。例えば、ニューラルネットワークの損失関数を最小化するパラメータを探す際、その勾配が \(0\) になる点を探すことは、まさに非線形方程式の根（解）を求める作業に他なりません。

非線形方程式は、ガウス消去法のように有限の手順で必ず解けるわけではありません。代わりに、適当な初期値から始めて、何度も計算を繰り返すことで正解へと近づけていく「反復法」を用います。今回は、最も堅牢な手法から、最も高速な手法まで、そのアルゴリズムの仕組みとPythonでの実装を丁寧に解説します。今回もよろしくお願いします。

1. はじめに：非線形方程式の根を求めるということ

非線形方程式 \(f(x) = 0\) を解くとは、グラフ上で曲線が \(x\) 軸と交わる点（根）を探す作業です。多くの場合、この \(x\) を代数的に（\(x = \dots\) の形に）求めることは不可能です。

そこで、近似値の数列 \(x_0, x_1, x_2, \dots\) を生成し、その極限が真の解 \(\alpha\) に重なるようにアルゴリズムを設計します。これを「数列の収束」と呼びます。

数値計算において「計算をいつ止めるか」は非常に重要です。無限に計算を続けるわけにはいかないため、通常は以下のいずれかの条件を満たしたときに終了します。

• \(|f(x_k)| < \epsilon\) （関数の値が十分に \(0\) に近い）
• \(|x_k – x_{k-1}| < \epsilon\) （解の変化が十分に小さくなった）
• 最大反復回数に達した（収束しなかった場合の保険）

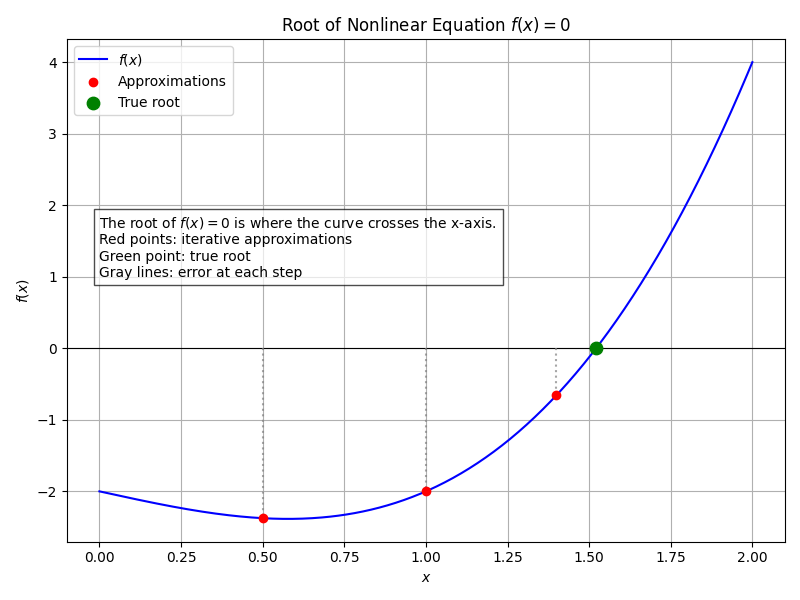
2. 確実な一歩：2分法（Bisection Method）

2分法（Bisection Method）は、非線形方程式 \(f(x) = 0\) の根を求めるための最も基本的かつ堅牢なアルゴリズムです。

この手法は「中間値の定理」に基づいています。すなわち、\(f(x)\) が連続関数であり、区間 \([a, b]\) の両端で関数値の符号が異なる（\(f(a) \cdot f(b) < 0\)）場合、必ずその区間内に少なくとも1つの根（\(f(x) = 0\) となる点）が存在します。

2分法の直感的なイメージは「根を含む区間を半分ずつ狭めていく」ことです。毎回、区間の中点を調べて、根がどちら側にあるかを判定し、探索範囲を半分に絞り込んでいきます。これを繰り返すことで、根の位置を任意の精度まで特定できます。

特徴と利点

• 確実性: 初期区間が正しく設定されていれば、必ず根に収束します。
• 単純さ: 実装が非常に簡単で、関数の微分や複雑な計算を必要としません。
• 数値的安定性: 丸め誤差や発散の心配がほとんどありません。

注意点・制約

• 収束速度: 1ステップごとに区間幅が半分になるため、収束は「1次収束」（線形収束）であり、他の手法（ニュートン法など）に比べて遅いです。
• 初期区間の選び方: \(f(a)\) と \(f(b)\) の符号が異なる区間を見つける必要があります。根が複数ある場合や、端点で関数値が0になる場合は注意が必要です。
• 連続性の仮定: 関数が不連続な場合や、区間内に根が複数ある場合は、期待通りに動作しないことがあります。

2分法は、理論的な堅牢性と実装の容易さから、数値計算の入門や「まずは確実に根の存在範囲を絞りたい」ときに非常に有用です。実務でも、他の高速な手法の初期値決定や、根の存在確認などに広く使われています。

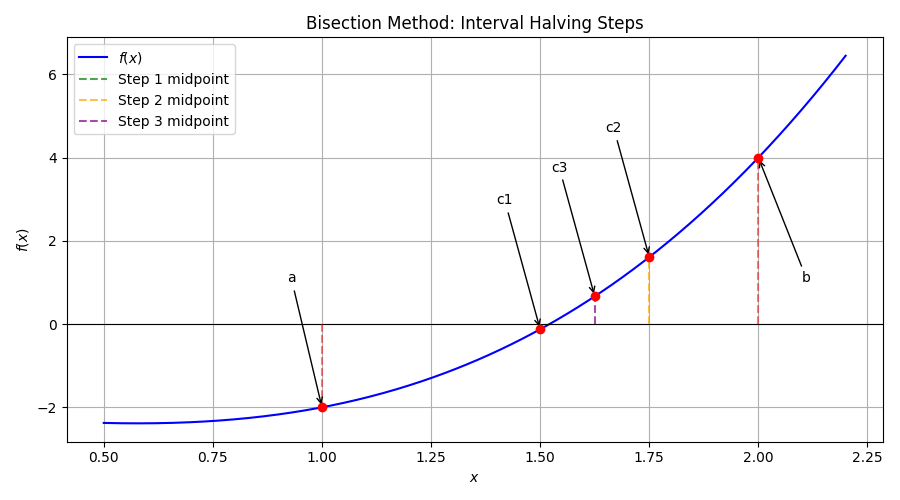
アルゴリズムの仕組み

1. 区間 \([a, b]\) の中点 \(c = (a+b)/2\) を求める。
2. \(f(c)\) の符号を確認する。
3. \(f(a)\) と \(f(c)\) の符号が異なれば、新しい区間を \([a, c]\) とする。そうでなければ \([c, b]\) とする。
4. 区間の幅が十分に小さくなるまで繰り返す。

2分法のPyTorch実装

import torch
import matplotlib.pyplot as plt
import numpy as np

def bisection_method(f, a, b, tol=1e-7, max_iter=100):
    fa = f(a)
    fb = f(b)
    if fa * fb > 0:
        raise ValueError("区間の端点で符号が同じです。根が存在するか不明です。")
    history = []
    for i in range(max_iter):
        c = (a + b) / 2
        fc = f(c)
        history.append(c.item())
        if torch.abs(fc) < tol or (b - a) / 2 < tol:
            return c, history
        if fa * fc < 0:
            b = c
            fb = fc
        else:
            a = c
            fa = fc
    return (a + b) / 2, history

def test_func(x):
    return x**3 - x - 2.0

root, hist = bisection_method(test_func, torch.tensor(1.0), torch.tensor(2.0))
print(f"Bisection Root: {root.item():.7f} (Found in {len(hist)} iterations)")

# グラフ化
x_range = np.linspace(1, 2, 100)
y_range = x_range**3 - x_range - 2
plt.plot(x_range, y_range, 'k', alpha=0.3)
plt.axhline(0, color='red', lw=0.5)
for i, val in enumerate(hist):
    plt.plot(val, 0, 'bo', markersize=i+1, alpha=0.5)

# 最終的な根を拡大表示するために、表示範囲を調整
# x軸の範囲を根の周りに設定
plt.xlim(root.item() - 0.01, root.item() + 0.01)
# y軸の範囲を0の周りに設定
plt.ylim(-0.01, 0.01)

# 最終的な根の位置を赤い星印で強調
plt.plot(root.item(), 0, 'r*', markersize=10, label='Final Root')

plt.title(f"Bisection Method Convergence (Zoomed, {len(hist)} steps)")
plt.xlabel("x")
plt.ylabel("f(x)")
plt.legend()
plt.grid(True)
plt.show()

import torch
import matplotlib.pyplot as plt
import numpy as np

def bisection_method(f, a, b, tol=1e-7, max_iter=100):
    fa = f(a)
    fb = f(b)
    if fa * fb > 0:
        raise ValueError("区間の端点で符号が同じです。根が存在するか不明です。")
    history = []
    for i in range(max_iter):
        c = (a + b) / 2
        fc = f(c)
        history.append(c.item())
        if torch.abs(fc) < tol or (b - a) / 2 < tol:
            return c, history
        if fa * fc < 0:
            b = c
            fb = fc
        else:
            a = c
            fa = fc
    return (a + b) / 2, history

def test_func(x):
    return x**3 - x - 2.0

root, hist = bisection_method(test_func, torch.tensor(1.0), torch.tensor(2.0))
print(f"Bisection Root: {root.item():.7f} (Found in {len(hist)} iterations)")

# グラフ化
x_range = np.linspace(1, 2, 100)
y_range = x_range**3 - x_range - 2
plt.plot(x_range, y_range, 'k', alpha=0.3)
plt.axhline(0, color='red', lw=0.5)
for i, val in enumerate(hist):
    plt.plot(val, 0, 'bo', markersize=i+1, alpha=0.5)

# 最終的な根を拡大表示するために、表示範囲を調整
# x軸の範囲を根の周りに設定
plt.xlim(root.item() - 0.01, root.item() + 0.01)
# y軸の範囲を0の周りに設定
plt.ylim(-0.01, 0.01)

# 最終的な根の位置を赤い星印で強調
plt.plot(root.item(), 0, 'r*', markersize=10, label='Final Root')

plt.title(f"Bisection Method Convergence (Zoomed, {len(hist)} steps)")
plt.xlabel("x")
plt.ylabel("f(x)")
plt.legend()
plt.grid(True)
plt.show()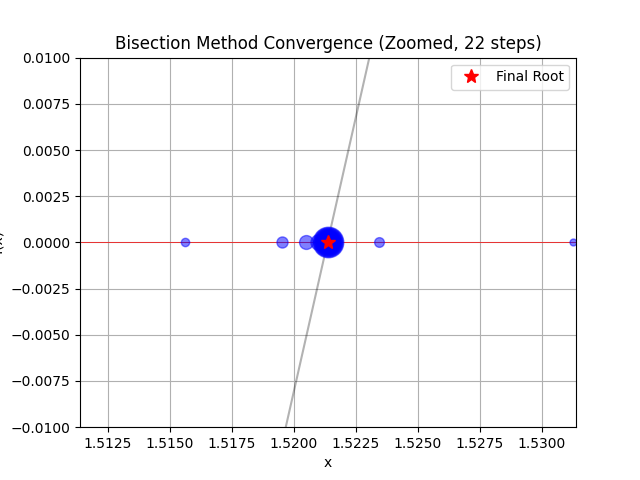

解説

2分法は、毎ステップで探索範囲が半分になります。これは「バイナリサーチ（二分探索）」と同じ原理です。非常に堅牢で、初期値さえ正しく選べば必ず収束しますが、収束速度は遅い（1次収束）という特徴があります。

3. 圧倒的なスピード：ニュートン法（Newton’s Method）

非線形方程式の解法において、王道とも言えるのがニュートン法です。2分法が「範囲を追い詰める」手法だったのに対し、ニュートン法は「現在の点での接線を頼りに、根の場所を予測する」手法です。

アルゴリズムの仕組み

現在の近似値 \(x_k\) における関数の接線を引き、その接線が \(x\) 軸と交わる点を次の近似値 \(x_{k+1}\) とします。
$$x_{k+1} = x_k – \frac{f(x_k)}{f'(x_k)}$$
これを繰り返すと、解の近くでは驚異的なスピードで真値に近づきます。

PyTorchの自動微分を活用したニュートン法

ニュートン法には関数の微分（導関数）が必要ですが、複雑な関数をいちいち手で微分するのは大変です。ここではPyTorchの autograd を使って、微分計算を自動化しましょう。

import matplotlib.pyplot as plt
import numpy as np

# グラフ化
x_range = np.linspace(min(hist_n) - 0.5, max(hist_n) + 0.5, 100) # 履歴に基づいて範囲を調整
y_range = test_func(torch.tensor(x_range))
plt.figure(figsize=(10, 6))
plt.plot(x_range, y_range, 'k-', alpha=0.5, label='f(x)')
plt.axhline(0, color='red', lw=0.8, linestyle='--')

# 各ステップの処理を表示
for i, val in enumerate(hist_n):
    func_val = test_func(torch.tensor(val)).item()
    # 各ステップの中点とf(中点)をプロット
    plt.plot(val, func_val, 'o', color='blue', markersize=5, alpha=0.6)
    # x軸から関数値までの垂直線
    plt.plot([val, val], [0, func_val], ':', color='gray', alpha=0.5)
    # x軸上の点
    plt.plot(val, 0, 'x', color='green', markersize=5, alpha=0.6)

    # イテレーション番号をプロット（引き出し線付き）
    # xytext の値を調整して、数字が重ならないようにする
    # xytext はイテレーション回数に応じて調整
    text_offset_y = 10 + i * 5 # 少しずつオフセットを増やす
    plt.annotate(str(i + 1),
                 xy=(val, func_val),
                 xytext=(val + 0.1, func_val + text_offset_y * 0.1), # テキストの位置を調整
                 textcoords='data', # データ座標を使用
                 arrowprops=dict(facecolor='black', shrink=0.05, width=0.5, headwidth=4, headlength=4, connectionstyle='arc3,rad=.2'),
                 fontsize=9,
                 color='darkblue')

# 最終的な根の位置を赤い星印で強調
plt.plot(root_n.item(), 0, 'r*', markersize=12, label='Final Root')

plt.title(f"Newton's Method Convergence Steps ({len(hist_n)} iterations)")
plt.xlabel("x")
plt.ylabel("f(x)")
plt.legend()
plt.grid(True)
plt.show()

import matplotlib.pyplot as plt
import numpy as np

# グラフ化
x_range = np.linspace(min(hist_n) - 0.5, max(hist_n) + 0.5, 100) # 履歴に基づいて範囲を調整
y_range = test_func(torch.tensor(x_range))
plt.figure(figsize=(10, 6))
plt.plot(x_range, y_range, 'k-', alpha=0.5, label='f(x)')
plt.axhline(0, color='red', lw=0.8, linestyle='--')

# 各ステップの処理を表示
for i, val in enumerate(hist_n):
    func_val = test_func(torch.tensor(val)).item()
    # 各ステップの中点とf(中点)をプロット
    plt.plot(val, func_val, 'o', color='blue', markersize=5, alpha=0.6)
    # x軸から関数値までの垂直線
    plt.plot([val, val], [0, func_val], ':', color='gray', alpha=0.5)
    # x軸上の点
    plt.plot(val, 0, 'x', color='green', markersize=5, alpha=0.6)

    # イテレーション番号をプロット（引き出し線付き）
    # xytext の値を調整して、数字が重ならないようにする
    # xytext はイテレーション回数に応じて調整
    text_offset_y = 10 + i * 5 # 少しずつオフセットを増やす
    plt.annotate(str(i + 1),
                 xy=(val, func_val),
                 xytext=(val + 0.1, func_val + text_offset_y * 0.1), # テキストの位置を調整
                 textcoords='data', # データ座標を使用
                 arrowprops=dict(facecolor='black', shrink=0.05, width=0.5, headwidth=4, headlength=4, connectionstyle='arc3,rad=.2'),
                 fontsize=9,
                 color='darkblue')

# 最終的な根の位置を赤い星印で強調
plt.plot(root_n.item(), 0, 'r*', markersize=12, label='Final Root')

plt.title(f"Newton's Method Convergence Steps ({len(hist_n)} iterations)")
plt.xlabel("x")
plt.ylabel("f(x)")
plt.legend()
plt.grid(True)
plt.show()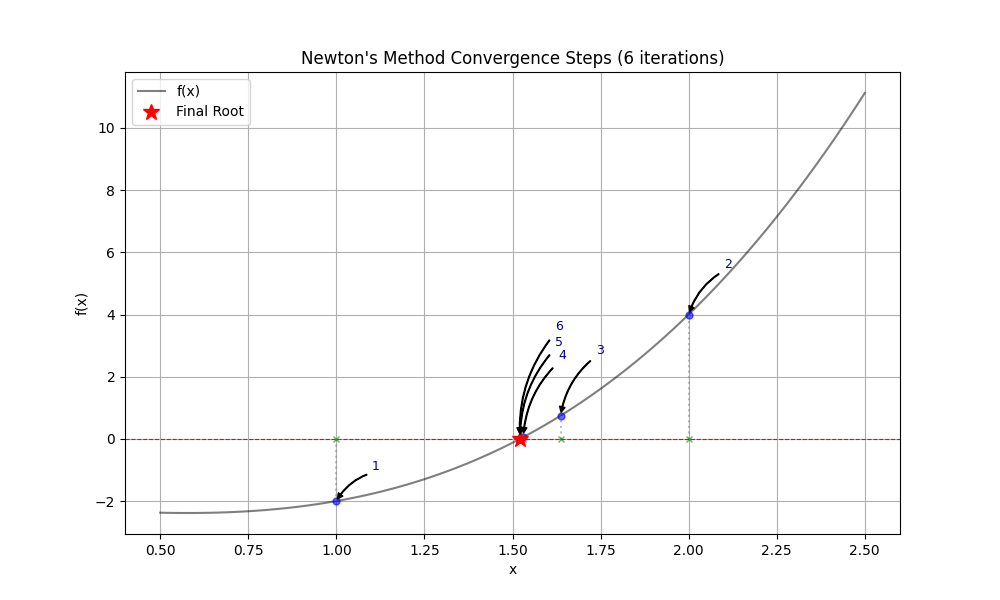

解説

ニュートン法の結果を見てください。2分法では20回以上かかった計算が、わずか数回で完了しています。これが「2次収束」の威力です。
ただし、ニュートン法には弱点もあります。

• 初期値が解から遠すぎると、接線が変な方向へ飛んでいき、収束しないことがある。
• 微分係数が \(0\) になる点の近くでは動作が不安定になる。

4. 微分が使えない時の選択肢：割線法（Secant Method）

ニュートン法は非常に強力な手法ですが、実際には「関数の微分が分からない」「微分の計算が非常に面倒・コストが高い」「関数自体がブラックボックスである」といった状況も多くあります。そんなときに活躍するのが「割線法（Secant Method）」です。

割線法は、ニュートン法の“微分”の部分を「過去2点の情報」から近似的に置き換えることで、微分計算を一切使わずに根を探すことができるアルゴリズムです。

割線法のアイデア

ニュートン法では、現在の点 \(x_k\) での接線（微分）を使って次の点 \(x_{k+1}\) を予測しますが、割線法では「直近2回の点 \(x_{k-1}\), \(x_k\) を通る直線（割線）」を使って \(x\) 軸との交点を次の点とします。

このときの更新式は次のようになります：
$$
x_{k+1} = x_k – f(x_k) \frac{x_k – x_{k-1}}{f(x_k) – f(x_{k-1})}
$$

この式は、\(f(x)\) のグラフ上で \((x_{k-1}, f(x_{k-1}))\) と \((x_k, f(x_k))\) を結ぶ直線（割線）が \(x\) 軸と交わる点を \(x_{k+1}\) として求めていることを意味します。

割線法の特徴と利点

• 微分不要: \(f(x)\) の値さえ計算できればよく、導関数 \(f'(x)\) の情報は一切不要です。
• 初期値は2つ必要: 2点から始めるため、\(x_0\) と \(x_1\) の2つの初期値が必要です。
• 収束速度: 2分法（線形収束）より速く、ニュートン法（2次収束）よりは遅い「1.6次収束」と呼ばれる中間的な速さです。
• 実装が簡単: 微分の実装や自動微分の準備が不要なため、ブラックボックス関数や実験データにも適用しやすいです。

割線法の注意点

• 2点の関数値が近いと不安定: \(f(x_k) \approx f(x_{k-1})\) となると分母が小さくなり、数値的に不安定になることがあります。
• 初期値の選び方が重要: 良い初期値を選ばないと収束しない場合もあります。
• 2分法のような「必ず区間内に根がある」保証はない: 収束性はニュートン法と同様、初期値に依存します。

割線法のイメージ

イメージとしては、

1. 最初に2つの点 \(x_0\), \(x_1\) を用意し、それぞれの \(f(x_0)\), \(f(x_1)\) を計算。
2. その2点を結ぶ直線（割線）を引き、その直線が \(x\) 軸と交わる点 \(x_2\) を計算。
3. \(x_1\), \(x_2\) を新たな2点として繰り返す。

このようにして、毎回「直近2点の情報」だけで次の点を予測していきます。

5. 実践：各手法の収束プロセスを可視化する

最後に、2分法とニュートン法がどのように解に近づいていくのか、その軌跡をグラフにして比較してみましょう。

import matplotlib.pyplot as plt
import numpy as np

def visualize_convergence():
    x_range = np.linspace(1, 2, 100)
    y_range = x_range**3 - x_range - 2

    plt.figure(figsize=(12, 5))

    # 2分法のプロット
    plt.subplot(1, 2, 1)
    plt.plot(x_range, y_range, 'k', alpha=0.3)
    plt.axhline(0, color='red', lw=0.5)
    for i, val in enumerate(hist):
        plt.plot(val, 0, 'bo', markersize=i+1, alpha=0.5)
    plt.title(f"Bisection Method Convåçergence ({len(hist)} steps)")
    plt.grid(True)

    # ニュートン法のプロット
    plt.subplot(1, 2, 2)
    plt.plot(x_range, y_range, 'k', alpha=0.3)
    plt.axhline(0, color='red', lw=0.5)
    for i, val in enumerate(hist_n):
        plt.plot(val, 0, 'go', markersize=(i+1)*2, alpha=0.5)
    plt.title(f"Newton's Method Convergence ({len(hist_n)} steps)")
    plt.grid(True)

    plt.tight_layout()
    plt.show()

visualize_convergence()

import matplotlib.pyplot as plt
import numpy as np

def visualize_convergence():
    x_range = np.linspace(1, 2, 100)
    y_range = x_range**3 - x_range - 2

    plt.figure(figsize=(12, 5))

    # 2分法のプロット
    plt.subplot(1, 2, 1)
    plt.plot(x_range, y_range, 'k', alpha=0.3)
    plt.axhline(0, color='red', lw=0.5)
    for i, val in enumerate(hist):
        plt.plot(val, 0, 'bo', markersize=i+1, alpha=0.5)
    plt.title(f"Bisection Method Convåçergence ({len(hist)} steps)")
    plt.grid(True)

    # ニュートン法のプロット
    plt.subplot(1, 2, 2)
    plt.plot(x_range, y_range, 'k', alpha=0.3)
    plt.axhline(0, color='red', lw=0.5)
    for i, val in enumerate(hist_n):
        plt.plot(val, 0, 'go', markersize=(i+1)*2, alpha=0.5)
    plt.title(f"Newton's Method Convergence ({len(hist_n)} steps)")
    plt.grid(True)

    plt.tight_layout()
    plt.show()

visualize_convergence()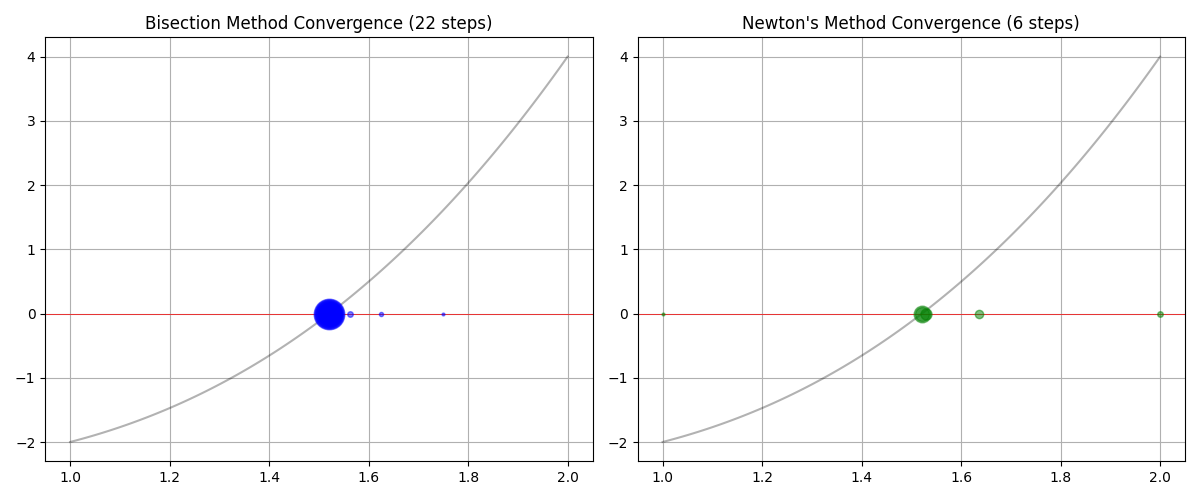

視覚的な比較

グラフを見ると、2分法が左右からじわじわと根を挟み込んでいるのに対し、ニュートン法は最初の数ステップで一気に根のすぐそばまでジャンプしているのがわかります。

実務においては、まず2分法で根の大まかな位置を特定し、その値を初期値としてニュートン法を走らせる、というハイブリッドなアプローチ（「はさみうち法」の改良版など）がよく取られます。

6. 実践的なアドバイス：SciPyのソルバー

自分で実装することでアルゴリズムの本質が理解できましたが、実際のプロジェクトでは SciPy の optimize モジュールを使うのが最も安全です。

from scipy import optimize


# 最も推奨される汎用ソルバー 'brentq'
# 2分法の安定性と逆二次補間による速さを兼ね備えています
root_scipy = optimize.brentq(lambda x: x**3 - x - 2, 1, 2)
print(f"SciPy root: {root_scipy:.7f}")

from scipy import optimize


# 最も推奨される汎用ソルバー 'brentq'
# 2分法の安定性と逆二次補間による速さを兼ね備えています
root_scipy = optimize.brentq(lambda x: x**3 - x - 2, 1, 2)
print(f"SciPy root: {root_scipy:.7f}")

SciPyの brentq は、今回学んだ手法の「いいとこ取り」をしたアルゴリズムで、多くの数値計算ライブラリで標準的に採用されています。

SciPy root: 1.5213797

SciPy root: 1.5213797

まとめ

第10回では、非線形方程式 \(f(x) = 0\) を解くための手法を学びました。

• 2分法は、中間値の定理に基づき、確実だがゆっくりと収束する。
• ニュートン法は、接線を利用して2次収束という圧倒的な速さを実現するが、初期値依存性と微分の必要性という課題がある。
• 割線法は、微分が困難な場合にニュートン法の代用として機能する。
• PyTorchの自動微分を組み合わせることで、複雑な非線形問題もシンプルに実装できる。

「方程式を解く」という行為は、AIモデルの学習そのものです。今回学んだ「反復して最適解に近づく」という感覚は、勾配降下法などの最適化アルゴリズムを理解する上でも大きな財産となります。

次回は、これまでの知識を総動員して、行列の本質的な性質を暴き出す「固有値問題の数値解法」に挑みます。累乗法や逆反復法など、データ分析で非常に重要なトピックです。お楽しみに。

最後まで読んでいただきありがとうございます。

連載記事、各回へのリンク

Pythonで学ぶ数値計算のアルゴリズムと実装 第1回：多項式計算とテイラー展開 | アマチュア無線局JS2IIU
https://js2iiu.com/2025/12/31/python_numerical_01/

Pythonで学ぶ数値計算のアルゴリズムと実装 第2回：多項式補間とチェビシェフ補間の戦略 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/01/python_numerical_02/

Pythonで学ぶ数値計算のアルゴリズムと実装 第3回：積分の基礎：中点則、台形則からシンプソン則まで | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/01/python_numerical_03/

Pythonで学ぶ数値計算のアルゴリズムと実装 第4回：高度な数値積分：二重指数型（DE）公式と広義積分 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/01/python_numerical_04/

Pythonで学ぶ数値計算のアルゴリズムと実装 第5回：計算の「正しさ」を評価する：ノルムと条件数 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/01/python_numeric_05/

Pythonで学ぶ数値計算のアルゴリズムと実装 第6回：連立一次方程式の直截解法：ガウス消去法とピボット選択 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/01/python_numerical_06/

Pythonで学ぶ数値計算のアルゴリズムと実装 第8回：スパース性を活かす：帯行列の高速計算アルゴリズム | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/02/python_numerical_08/

Pythonで学ぶ数値計算のアルゴリズムと実装 第9回：最小二乗法とQR分解：ハウスホルダー変換による安定化 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/02/python_numerial_09/

Pythonで学ぶ数値計算のアルゴリズムと実装 第10回：非線形方程式の探索：2分法からニュートン法まで | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/03/python_numerical_10/

Pythonで学ぶ数値計算のアルゴリズムと実装 第11回：行列の本質を捉える：固有値問題の数値解法 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/03/python_numerical_11/

Pythonで学ぶ数値計算のアルゴリズムと実装 第12回：現象の変化を追う：ルンゲ・クッタ法による常微分方程式の解法 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/03/python_numerical_12/

Pythonで学ぶ数値計算のアルゴリズムと実装 第13回：空間の熱と振動を解く：偏微分方程式の差分近似と反復解法 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/03/python_numerical_13/