Pythonで学ぶ数値計算のアルゴリズムと実装 第11回：行列の本質を捉える：固有値問題の数値解法

こんにちは、JS2IIUです。
数値計算連載の第11回目となる今回は、線形代数の華とも言える「固有値問題（Eigenvalue Problem）」の数値解法に焦点を当てます。

機械学習を学ぶ中で「主成分分析（PCA）」や「スペクトラルクラスタリング」、あるいは「GoogleのPageRankアルゴリズム」といった言葉を耳にしたことがあるでしょう。これらの技術の背後には、常に行列の固有値と固有ベクトルが潜んでいます。固有値とは、行列という「線形変換」が空間をどの方向に、どれだけ引き伸ばすのかという「行列の本質」を象徴する値です。

理論上は、固有値は特性方程式 \(\det(A – \lambda I) = 0\) を解くことで求められますが、実用的なサイズの行列に対してこの方程式を直接解くことは不可能です。そのため、コンピュータを用いた反復的な数値解法が必要となります。今回は、最も基本的かつ強力な「累乗法」と、特定の固有値を狙い撃ちする「逆反復法」を中心に、そのアルゴリズムと実装を詳しく見ていきましょう。今回もよろしくお願いします。

1. はじめに：固有値・固有ベクトルがなぜ重要か

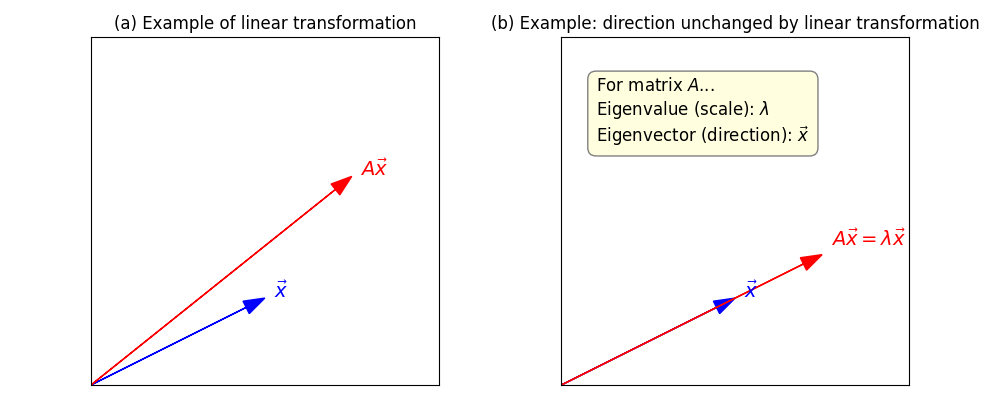
行列 \(A\) をベクトル \(x\) に掛けるという操作は、空間を回転させたり、引き伸ばしたりする操作に対応します。多くのベクトルは、行列を掛けられると向きが変わってしまいますが、中には「向きが変わらず、長さだけが変わる」という特別なベクトルが存在します。それが固有ベクトルであり、その変化倍率が固有値です。

固有値・固有ベクトルの具体的イメージ

例えば、2次元の平面上で「回転」や「拡大・縮小」といった操作を行う行列 \(A\) を考えます。ほとんどのベクトル \(x\) は、\(A\) を掛けると向きも長さも変わります。しかし、特定のベクトル \(v\) だけは、\(A\) を掛けても「向きはそのまま」で「長さだけが変わる」ことがあります。このようなベクトル \(v\) を「固有ベクトル」と呼び、その時の倍率 \(\lambda\) を「固有値」と呼びます。式で表すと \(A v = \lambda v\) です。

具体例：

• \(A\) が「拡大縮小」だけを行う行列なら、すべてのベクトルが固有ベクトルになります。
• \(A\) が「回転」だけを行う行列なら、実数の固有ベクトルは存在しません（複素数なら存在）。
• \(A\) が「斜め方向に引き伸ばす」行列なら、引き伸ばし方向のベクトルだけが固有ベクトルになります。

このように、固有ベクトルは「変換の本質的な軸」を示し、固有値は「その軸方向でどれだけ伸び縮みするか」を表します。主成分分析（PCA）やPageRankなどの応用では、「データやネットワークの中で最も重要な方向や要素」を抽出するために、固有値・固有ベクトルが使われています。

例えば、データ分析における主成分分析（PCA）では、データのバラつきが最も大きい方向を探しますが、これはデータ共分散行列の「最大固有値に対応する固有ベクトル」を求めることと同義です。また、大規模なネットワークの重要度を測るPageRankは、巨大な遷移確率行列の固有ベクトルを求める問題に帰着します。

このように、行列のすべてを計算するのではなく、「最も支配的な性質（固有値）」だけを効率的に抜き出す技術は、現代のAI技術を支える基盤となっています。

2. 最大固有値を追い詰める：累乗法（Power Method）

累乗法は、行列の中で絶対値が最大の固有値（主固有値）とその固有ベクトルを求めるための最もシンプルなアルゴリズムです。

アルゴリズムの直感的理解

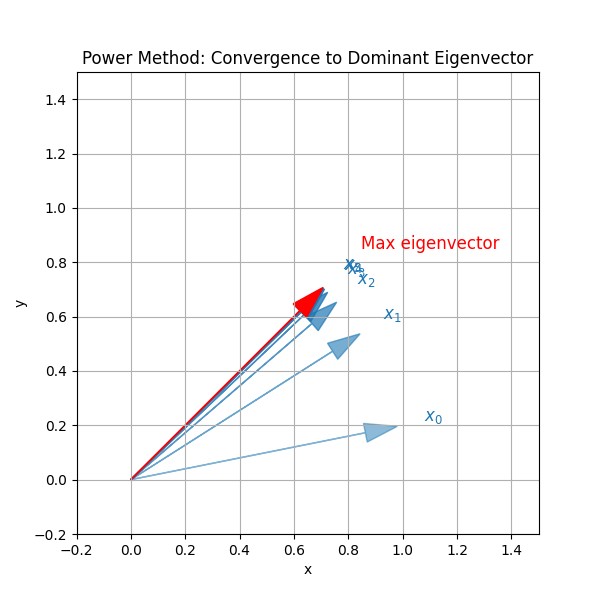
累乗法の本質は「繰り返し行列を掛けることで、最大固有値の方向を強調していく」ことです。

まず、初期ベクトル \(x_0\) は、一般的には行列 \(A\) のすべての固有ベクトルの成分を少しずつ含んでいます。行列 \(A\) を掛ける操作 \(x_{k+1} = Ax_k\) を何度も繰り返すと、各固有ベクトル成分はそれぞれの固有値によって伸び縮みします。

特に、最大固有値 \(\lambda_1\) に対応する成分は、他の固有値よりも速く（大きく）伸びていくため、反復を重ねるごとに「最大固有値の方向」がどんどん強調されていきます。最終的には、初期ベクトルに含まれていた他の固有ベクトル成分は相対的に小さくなり、ベクトルは最大固有値に対応する固有ベクトルの向きへと収束します。

この収束の速さは、最大固有値と次に大きい固有値の比 \(|\lambda_2/\lambda_1|\) に依存します。比が小さいほど、収束は速くなります。

また、毎回ベクトルの長さを正規化することで、数値的なオーバーフローを防ぎつつ、向きの変化だけに注目できるようになります。

このように、累乗法は「行列の本質的な方向（最大固有値）」を効率的に抽出するための、非常にシンプルかつ強力な手法です。

累乗法のPyTorch実装

数値計算上の注意点として、そのまま掛け続けるとベクトルの要素が無限に大きくなってしまう（オーバーフローする）ため、各ステップでベクトルの長さを \(1\) に正規化する必要があります。

import torch

def power_method(A, max_iter=1000, tol=1e-8):
    """
    累乗法を用いて、行列 A の最大固有値と固有ベクトルを求める

    Args:
        A (torch.Tensor): 正方行列
        max_iter (int): 最大反復回数
        tol (float): 収束判定の許容誤差

    Returns:
        eigenvalue (float): 最大固有値の近似値
        eigenvector (torch.Tensor): 対応する固有ベクトル
    """
    n = A.shape[0]
    # 初期ベクトルをランダムに生成し、正規化する
    x = torch.randn(n, 1, device=A.device, dtype=A.dtype)
    x = x / torch.norm(x)

    prev_lambda = 0.0

    for i in range(max_iter):
        # 行列を掛ける (Ax)
        x_next = torch.matmul(A, x)

        # レイリー商を用いて固有値を推定: λ = (x^T Ax) / (x^T x)
        # xは正規化されているので λ = x^T @ x_next
        eigenvalue = torch.matmul(x.t(), x_next).item()

        # ベクトルを正規化する
        x = x_next / torch.norm(x_next)

        # 収束判定
        if abs(eigenvalue - prev_lambda) < tol:
            print(f"Power Method: converged at iteration {i}")
            return eigenvalue, x

        prev_lambda = eigenvalue

    return prev_lambda, x

# テスト用の行列
A_test = torch.tensor([[4.0, 1.0, 2.0],
                       [1.0, 3.0, 0.0],
                       [2.0, 0.0, 5.0]])

val, vec = power_method(A_test)
print(f"Dominant Eigenvalue: {val:.6f}")

import torch

def power_method(A, max_iter=1000, tol=1e-8):
    """
    累乗法を用いて、行列 A の最大固有値と固有ベクトルを求める

    Args:
        A (torch.Tensor): 正方行列
        max_iter (int): 最大反復回数
        tol (float): 収束判定の許容誤差

    Returns:
        eigenvalue (float): 最大固有値の近似値
        eigenvector (torch.Tensor): 対応する固有ベクトル
    """
    n = A.shape[0]
    # 初期ベクトルをランダムに生成し、正規化する
    x = torch.randn(n, 1, device=A.device, dtype=A.dtype)
    x = x / torch.norm(x)

    prev_lambda = 0.0

    for i in range(max_iter):
        # 行列を掛ける (Ax)
        x_next = torch.matmul(A, x)

        # レイリー商を用いて固有値を推定: λ = (x^T Ax) / (x^T x)
        # xは正規化されているので λ = x^T @ x_next
        eigenvalue = torch.matmul(x.t(), x_next).item()

        # ベクトルを正規化する
        x = x_next / torch.norm(x_next)

        # 収束判定
        if abs(eigenvalue - prev_lambda) < tol:
            print(f"Power Method: converged at iteration {i}")
            return eigenvalue, x

        prev_lambda = eigenvalue

    return prev_lambda, x

# テスト用の行列
A_test = torch.tensor([[4.0, 1.0, 2.0],
                       [1.0, 3.0, 0.0],
                       [2.0, 0.0, 5.0]])

val, vec = power_method(A_test)
print(f"Dominant Eigenvalue: {val:.6f}")

Power Method: converged at iteration 18
Dominant Eigenvalue: 6.669079

Power Method: converged at iteration 18
Dominant Eigenvalue: 6.669079

解説

累乗法の計算量は、各ステップで行列とベクトルの積を行うため \(O(n^2)\) です。これを \(k\) 回繰り返すので全体では \(O(k n^2)\) となります。全固有値を求める手法（QR法など）が \(O(n^3)\) 必要であることを考えると、非常に巨大な行列に対して最大のものだけを知りたい場合には圧倒的に効率的です。

3. 狙った固有値を抽出する：逆反復法（Inverse Iteration）

累乗法は「最大固有値」しか見つけられませんが、現実の応用では「最小固有値」や「特定の値 \(\alpha\) に近い固有値」を知りたい場面が多くあります。例えば、安定性解析や物理シミュレーションでは最小固有値が重要になることが多いです。

逆反復法の基本的な考え方は、「行列 \(A\) の逆行列 \(A^{-1}\) を使えば、\(A\) の最小固有値が \(A^{-1}\) の最大固有値になる」という性質を利用することです。累乗法と同じように \(A^{-1}\) を何度も掛けることで、\(A\) の最小固有値に対応する固有ベクトルの方向へと収束します。

さらに、\(A\) から \(\mu I\) を引いた行列 \(A – \mu I\) の逆行列を使うことで、「\(\mu\) に最も近い固有値」を狙い撃ちできます。これを「シフト付き逆反復法」と呼びます。\(\mu\) を変えることで、任意の領域の固有値を効率よく抽出できるのが大きな特徴です。

実際の計算では、逆行列そのものを毎回計算するのは非常にコストが高いため、LU分解などを使って「連立一次方程式 \((A – \mu I)x_{k+1} = x_k\) を解く」ことで、効率的に反復を進めます。これにより、計算量を大幅に削減できます。

このように逆反復法は、「最大固有値」以外の固有値を柔軟に抽出できる強力な手法であり、数値線形代数の現場で非常によく使われています。

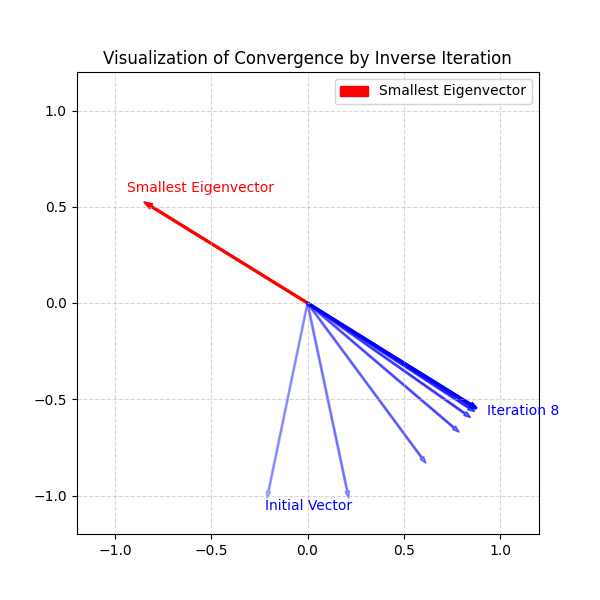
アルゴリズムの仕組み

行列 \(A\) の固有値が \(\lambda\) であるとき、逆行列 \(A^{-1}\) の固有値は \(1/\lambda\) になります。つまり、\(A\) の最小固有値は、\(A^{-1}\) にとっての最大固有値になります。
これを利用して、逆行列を繰り返し掛ける操作を行えば、最小固有値へと収束します。

実際には、逆行列そのものを計算するのは非効率なため、前回の連載（第6回、第7回）で学んだLU分解を利用して、連立一次方程式 \(A x_{k+1} = x_k\) を解くことで次のベクトルを求めます。

def inverse_iteration(A, mu=0.0, max_iter=1000, tol=1e-8):
    """
    逆反復法を用いて、指定した値 mu に最も近い固有値を求める
     mu=0 の場合は最小固有値を求めることになる
    """
    n = A.shape[0]
    # (A - mu*I) の固有値を狙うことで任意の近傍を探索できる
    A_shifted = A - mu * torch.eye(n, device=A.device, dtype=A.dtype)

    # LU分解を事前に行っておき、各ステップでの計算を O(n^2) にする
    LU, pivots = torch.linalg.lu_factor(A_shifted)

    x = torch.randn(n, 1, device=A.device, dtype=A.dtype)
    x = x / torch.norm(x)

    prev_lambda = 0.0

    for i in range(max_iter):
        # 連立方程式を解く: (A - mu*I) * x_next = x
        x_next = torch.linalg.lu_solve(LU, pivots, x)

        # 正規化
        x_norm = torch.norm(x_next)
        x = x_next / x_norm

        # 元の行列 A に対するレイリー商で固有値を推定
        eigenvalue = torch.matmul(torch.matmul(x.t(), A), x).item()

        if abs(eigenvalue - prev_lambda) < tol:
            print(f"Inverse Iteration: converged at iteration {i}")
            return eigenvalue, x

        prev_lambda = eigenvalue

    return prev_lambda, x

val_min, vec_min = inverse_iteration(A_test, mu=0.0)
print(f"Smallest Eigenvalue: {val_min:.6f}")

def inverse_iteration(A, mu=0.0, max_iter=1000, tol=1e-8):
    """
    逆反復法を用いて、指定した値 mu に最も近い固有値を求める
     mu=0 の場合は最小固有値を求めることになる
    """
    n = A.shape[0]
    # (A - mu*I) の固有値を狙うことで任意の近傍を探索できる
    A_shifted = A - mu * torch.eye(n, device=A.device, dtype=A.dtype)

    # LU分解を事前に行っておき、各ステップでの計算を O(n^2) にする
    LU, pivots = torch.linalg.lu_factor(A_shifted)

    x = torch.randn(n, 1, device=A.device, dtype=A.dtype)
    x = x / torch.norm(x)

    prev_lambda = 0.0

    for i in range(max_iter):
        # 連立方程式を解く: (A - mu*I) * x_next = x
        x_next = torch.linalg.lu_solve(LU, pivots, x)

        # 正規化
        x_norm = torch.norm(x_next)
        x = x_next / x_norm

        # 元の行列 A に対するレイリー商で固有値を推定
        eigenvalue = torch.matmul(torch.matmul(x.t(), A), x).item()

        if abs(eigenvalue - prev_lambda) < tol:
            print(f"Inverse Iteration: converged at iteration {i}")
            return eigenvalue, x

        prev_lambda = eigenvalue

    return prev_lambda, x

val_min, vec_min = inverse_iteration(A_test, mu=0.0)
print(f"Smallest Eigenvalue: {val_min:.6f}")

Inverse Iteration: converged at iteration 17
Smallest Eigenvalue: 1.854897

Inverse Iteration: converged at iteration 17
Smallest Eigenvalue: 1.854897

解説

逆反復法では、シフト値 \(\mu\) を適切に設定することで、任意の領域の固有値を高速に抽出できます。ここでは、第7回で解説した「LU分解を使い回す」というテクニックが、反復計算の高速化に直結していることがわかります。

4. 近似固有値の「正しさ」を測る：誤差評価

数値計算の結果が得られたとき、それがどれくらい正しいのかを判断する指標が必要です。

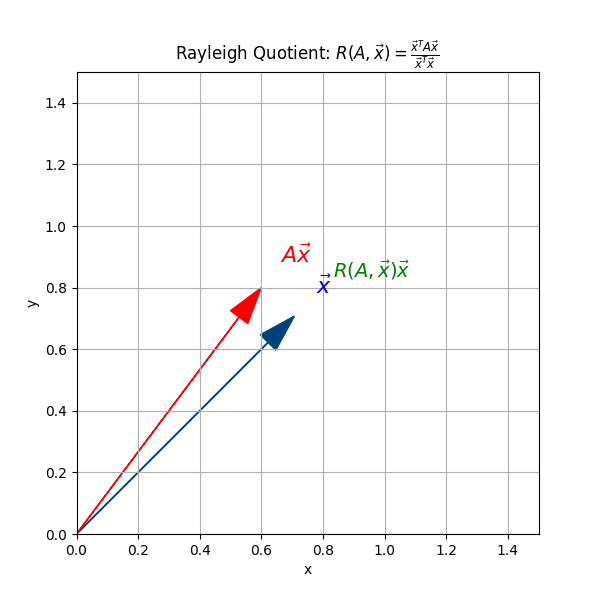
レイリー商（Rayleigh Quotient）

固有ベクトルの近似 \(x\) が得られたとき、最も確からしい固有値の推定値は、以下のレイリー商で与えられます。
$$R(A, x) = \frac{x^T A x}{x^T x}$$
この値は、真の固有値に対する最良の近似となり、誤差は固有ベクトルの誤差の2乗のオーダーで小さくなります。

レイリー商は、任意のベクトル \(x\) に対して「\(x\) がどれくらい行列 \(A\) の固有ベクトルに近いか」を測る指標でもあります。もし \(x\) が \(A\) の固有ベクトルそのものであれば、レイリー商は対応する固有値そのものになります。

なぜこれが固有値の近似になるかというと、\(A x = \lambda x\) ならば \(R(A, x) = \lambda\) となるからです。実際の数値計算では、\(x\) は厳密な固有ベクトルではなく近似値ですが、レイリー商を使うことで「今の \(x\) がどの固有値に近いか」を高精度に推定できます。

また、レイリー商は「最急降下法」や「レイリー商反復法」など、より高度な固有値計算アルゴリズムの基礎にもなっています。特に対称行列の場合、レイリー商は最小値・最大値問題とも深い関係があり、物理や工学の分野でも広く応用されています。

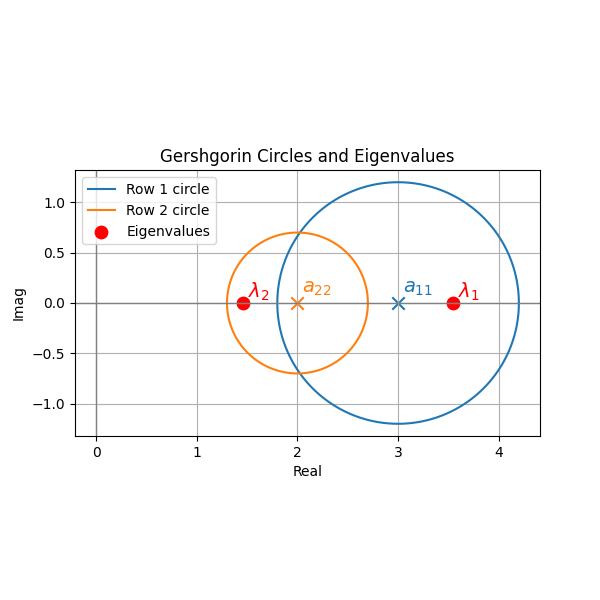
ゲシュゴリンの円定理（Gershgorin Circle Theorem）

行列の成分を見るだけで、固有値が「どの範囲に存在するか」を予測する強力な定理があります。
各行 \(i\) について、対角成分 \(a_{ii}\) を中心とし、その行の他の成分の絶対値の和を半径 \(R_i\) とする円を複素平面上に描くと、すべての固有値はいずれかの円の中に含まれます。

これは、大規模な行列計算を始める前に、「そもそも答えはどのあたりにあるのか」という目星をつけるための「健康診断」として非常に有用です。

ゲシュゴリンの円定理は、\(n \times n\) 行列 \(A = (a_{ij})\) の固有値が「どの範囲に存在するか」を、行列の成分だけから簡単に推定できる強力な理論です。

具体的には、各行 \(i\) について、
$$R_i = \sum_{j \neq i} |a_{ij}|$$
とし、複素平面上で「中心 \(a_{ii}\)、半径 \(R_i\)」の円（ゲシュゴリン円）を描きます。ゲシュゴリンの円定理は、「すべての固有値は、これら \(n\) 個の円のいずれかに必ず含まれる」と主張します。

この定理の直感は、「対角成分 \(a_{ii}\) が大きく、他の成分が小さいほど、固有値は \(a_{ii}\) の近くにある」というものです。特に対角優位な行列では、固有値の位置をかなり正確に予測できます。

応用例としては、数値計算で「固有値の初期推定」や「行列の安定性判定」などに使われます。また、円が重なっていなければ、固有値の分離性も保証できます。

ただし、ゲシュゴリンの円は「固有値の存在範囲の上限」を与えるものであり、実際の固有値が円の中心に近いとは限りません。あくまで「目安」として使うのがポイントです。

5. 実践的なアドバイス：SciPyとPyTorchの使い分け

ここまで反復法を自作してきましたが、実務において全固有値が必要な場合は、ライブラリの高度に最適化されたルーチンを使います。

# PyTorchでの全固有値計算 (対称行列の場合)
# torch.linalg.eigh は内部で高度な分割統治法などを使用しています
vals, vecs = torch.linalg.eigh(A_test)
print("All Eigenvalues (PyTorch):", vals)

# SciPyでの計算 (巨大な疎行列の場合)
from scipy.sparse.linalg import eigs
# 巨大な行列から「上位k個」だけを取り出すなど、
# まさに今回学んだ反復法の精神が活かされています

# PyTorchでの全固有値計算 (対称行列の場合)
# torch.linalg.eigh は内部で高度な分割統治法などを使用しています
vals, vecs = torch.linalg.eigh(A_test)
print("All Eigenvalues (PyTorch):", vals)

# SciPyでの計算 (巨大な疎行列の場合)
from scipy.sparse.linalg import eigs
# 巨大な行列から「上位k個」だけを取り出すなど、
# まさに今回学んだ反復法の精神が活かされています

自作した累乗法は、単に「仕組みを知る」ためだけのものではありません。例えば、ニューラルネットワークの「スペクトル正規化（Spectral Normalization）」という技術では、重み行列の最大固有値を計算するために、まさにこの累乗法が毎ステップの学習プロセスに組み込まれています。

6. 計算量と収束の性質

固有値問題の数値解法では、「どれだけ速く正しい固有値・固有ベクトルにたどり着けるか」が重要な指標となります。特に累乗法の収束速度は、行列の「固有値の分離度」に大きく左右されます。

累乗法では、初期ベクトルがすべての固有ベクトル成分を持っていると仮定すると、反復ごとに最大固有値 \(\lambda_1\) に対応する成分が指数関数的に強調されていきます。理論的には、\(k\) 回反復したときの誤差は \(|\lambda_2/\lambda_1|^k\) に比例して減少します。したがって、\(|\lambda_2/\lambda_1|\) が1に近い（固有値が接近している）場合は収束が遅く、0に近いほど急速に収束します。

この「分離度」は、他の反復型固有値アルゴリズム（逆反復法やレイリー商反復法など）でも重要な役割を果たします。逆反復法では、シフト値 \(\mu\) をうまく選ぶことで、任意の固有値近傍への高速収束が可能です。

また、計算量の観点では、累乗法は1回の反復で \(O(n^2)\)、全体で \(O(kn^2)\) ですが、全固有値を求めるQR法などは \(O(n^3)\) かかります。巨大な行列で「一番大きい（または小さい）固有値だけ知りたい」場合、累乗法や逆反復法は非常に効率的です。

実務では、行列の性質（対称性・疎性・分離度など）を見極めて、最適なアルゴリズムやパラメータを選ぶことが求められます。特に分離度が悪い場合は、初期ベクトルの工夫やシフト戦略、前処理なども重要になります。

まとめ

第11回では、行列の深層を探るための「固有値問題」の数値解法を学びました。

• 固有値・固有ベクトルは、線形変換の本質的な軸と倍率を表す。
• 累乗法は、行列の掛け算と正規化を繰り返すことで、効率的に最大固有値を抽出する。
• 逆反復法は、LU分解と組み合わせることで、最小あるいは特定の固有値を狙い撃ちできる。
• レイリー商やゲシュゴリンの円定理は、得られた結果の正しさを評価するための強力なツールである。

固有値の世界は、抽象的な数学に見えて、実はデータから価値ある情報を取り出すための「究極のフィルター」としての役割を担っています。

次回からは、いよいよ物理現象や時間の変化を記述する「常微分方程式」の数値解法に足を踏み入れます。有名なルンゲ・クッタ法など、シミュレーション技術の核心に迫ります。お楽しみに。

最後まで読んでいただきありがとうございます。

連載記事、各回へのリンク

Pythonで学ぶ数値計算のアルゴリズムと実装 第1回：多項式計算とテイラー展開 | アマチュア無線局JS2IIU
https://js2iiu.com/2025/12/31/python_numerical_01/

Pythonで学ぶ数値計算のアルゴリズムと実装 第2回：多項式補間とチェビシェフ補間の戦略 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/01/python_numerical_02/

Pythonで学ぶ数値計算のアルゴリズムと実装 第3回：積分の基礎：中点則、台形則からシンプソン則まで | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/01/python_numerical_03/

Pythonで学ぶ数値計算のアルゴリズムと実装 第4回：高度な数値積分：二重指数型（DE）公式と広義積分 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/01/python_numerical_04/

Pythonで学ぶ数値計算のアルゴリズムと実装 第5回：計算の「正しさ」を評価する：ノルムと条件数 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/01/python_numeric_05/

Pythonで学ぶ数値計算のアルゴリズムと実装 第6回：連立一次方程式の直截解法：ガウス消去法とピボット選択 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/01/python_numerical_06/

Pythonで学ぶ数値計算のアルゴリズムと実装 第8回：スパース性を活かす：帯行列の高速計算アルゴリズム | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/02/python_numerical_08/

Pythonで学ぶ数値計算のアルゴリズムと実装 第9回：最小二乗法とQR分解：ハウスホルダー変換による安定化 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/02/python_numerial_09/

Pythonで学ぶ数値計算のアルゴリズムと実装 第10回：非線形方程式の探索：2分法からニュートン法まで | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/03/python_numerical_10/

Pythonで学ぶ数値計算のアルゴリズムと実装 第11回：行列の本質を捉える：固有値問題の数値解法 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/03/python_numerical_11/

Pythonで学ぶ数値計算のアルゴリズムと実装 第12回：現象の変化を追う：ルンゲ・クッタ法による常微分方程式の解法 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/03/python_numerical_12/

Pythonで学ぶ数値計算のアルゴリズムと実装 第13回：空間の熱と振動を解く：偏微分方程式の差分近似と反復解法 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/03/python_numerical_13/