こんにちは、JS2IIUです。
数値計算連載の第12回となる今回は、シミュレーション技術の核心であり、現代のAI技術、特に「Neural ODE(神経常微分方程式)」などの基盤ともなっている「常微分方程式(Ordinary Differential Equations, ODE)」の数値解法を扱います。
物理学における物体の運動、化学反応の進行、経済学における市場の変動、そして生物学における人口動態。これら「時間の経過とともに変化する現象」の多くは、常微分方程式という言葉で記述されます。微分方程式を解くということは、現在の状態から未来の状態を予測することに他なりません。
理論的に厳密な解(一般解)が得られるケースは限られていますが、数値計算アルゴリズムを駆使すれば、コンピュータ上で未来の挙動を驚くべき精度で再現できます。今回は、最も基本的なオイラー法から、数値シミュレーションの標準である「ルンゲ・クッタ法」まで、その仕組みとPythonによる実装を深く掘り下げていきましょう。今回もよろしくお願いします。
1. はじめに:微分方程式を数値的に解くとは?
私たちが解きたいのは、以下のような形式の方程式です。
$$\frac{dy}{dt} = f(t, y), \quad y(t_0) = y_0$$
これは、「時刻 \(t\) における変化率(勾配)が、その時の時刻と状態 \(y\) によって決まる」というルールを示しています。数値解法では、時間を小さな刻み幅 \(h\)(ステップサイズ)で区切り、現在の状態 \(y_n\) から次の状態 \(y_{n+1}\) を順番に求めていきます。
これは、霧の中で手元のコンパス(微分方程式 \(f\))だけを頼りに、一歩ずつ目的地(未来)へ進む作業に例えられます。一歩を大きくすれば早く進めますが、道を踏み外す(誤差が溜まる)リスクが高まります。
2. オイラー法:最もシンプルな出発点
オイラー法は、常微分方程式(ODE)を数値的に解くための最も基本的な手法です。微分方程式
$$\frac{dy}{dt} = f(t, y), \quad y(t_0) = y_0$$
の解を、離散的なステップで近似的に求めます。
オイラー法のアルゴリズム
- 現在の時刻 \(t_n\) と状態 \(y_n\) から、微分方程式 \(f(t_n, y_n)\) を使って「次の瞬間の変化量」を計算します。
- ステップ幅 \(h\) を使って、次の状態 \(y_{n+1}\) を
$$
y_{n+1} = y_n + h \cdot f(t_n, y_n)
$$
で更新します。
この「現在の勾配をそのまま使って一歩進む」考え方は、グラフ上で接線方向に直線的に進むイメージです。
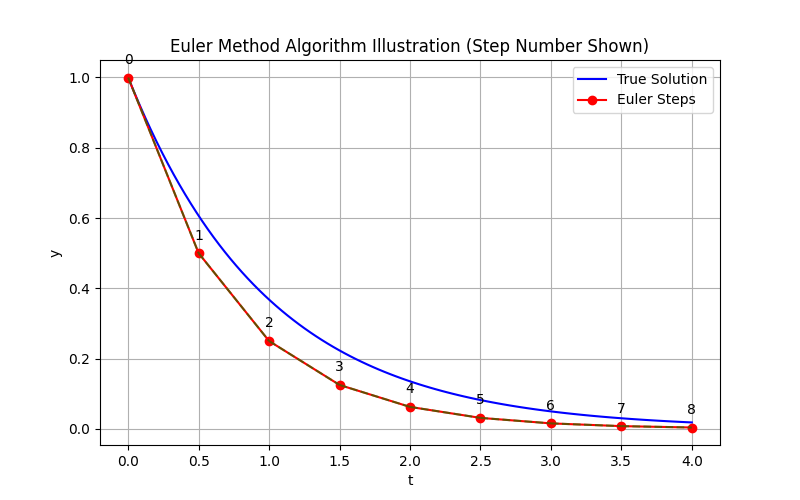
直感的な理解
- 例えば、坂道を歩いているときに「今の傾きのまま、一定距離だけ進む」と仮定するのがオイラー法です。
- しかし、実際の坂道は曲がっていることが多く、傾き(勾配)は進むにつれて変化します。オイラー法はこの変化を無視するため、誤差が蓄積しやすいです。
精度と限界
- オイラー法は「1次精度」しかありません。つまり、ステップ幅 \(h\) を小さくすればするほど精度は上がりますが、計算回数が増えてしまいます。
- \(h\) を大きくすると、誤差が急激に増え、解が発散したり、真の解から大きく外れることがあります。
AIとの関連
- オイラー法の更新式は、機械学習の「勾配降下法(Gradient Descent)」と同じ構造です。学習率 \(h\) を使って、現在のパラメータを勾配方向に更新する点が共通しています。
オイラー法のまとめ
- オイラー法は実装が非常に簡単で、数値計算の入門に最適です。
- ただし、精度や安定性の面では限界があるため、実用的なシミュレーションにはより高精度な手法(例:ルンゲ・クッタ法)が推奨されます。
3. ルンゲ・クッタ法(RK4):数値計算の王道
オイラー法の弱点は、「一歩進む間の勾配の変化を無視している」点にあります。これに対し、ルンゲ・クッタ法(特に一般的な4次の公式、RK4)は、一歩進む途中の地点で何度か「試しに勾配を測る」ことで、より正確な進むべき方向を決定します。
RK4のアルゴリズム
RK4(4次のルンゲ・クッタ法)は、オイラー法の「一歩進む間の勾配の変化を無視する」という弱点を克服するために考案された、非常に精度の高い数値解法です。
RK4の計算手順
1ステップで \(y_n\) から \(y_{n+1}\) へ進む際、途中の点で何度も勾配(微分値)を評価し、それらを重み付き平均して次の値を決定します。
具体的には、以下の4つの勾配 \(k_1, k_2, k_3, k_4\) を計算します。
- \(k_1\): 現在地 \((t_n, y_n)\) での勾配。
$$k_1 = f(t_n, y_n)$$
これはオイラー法と同じで、まず現時点の変化率を取得します。 - \(k_2\): \(k_1\) を使って半分ステップ進んだ仮想的な位置 \((t_n + h/2, y_n + h/2 \cdot k_1)\) での勾配。
$$k_2 = f\left(t_n + \frac{h}{2}, y_n + \frac{h}{2} k_1\right)$$
ここで「もし \(k_1\) の勾配で半分だけ進んだら?」という仮定のもと、次の勾配を測ります。 - \(k_3\): \(k_2\) を使ってさらに半分ステップ進んだ仮想的な位置 \((t_n + h/2, y_n + h/2 \cdot k_2)\) での勾配。
$$k_3 = f\left(t_n + \frac{h}{2}, y_n + \frac{h}{2} k_2\right)$$
2回目の「仮想的な半分進み」で、より現実的な勾配を取得します。 - \(k_4\): \(k_3\) を使って1ステップ進んだ仮想的な位置 \((t_n + h, y_n + h \cdot k_3)\) での勾配。
$$k_4 = f(t_n + h, y_n + h k_3)$$
最後に「もし \(k_3\) の勾配で1ステップ進んだら?」という仮定で勾配を測ります。
これら4つの勾配を、重み付き平均(\(k_1:1, k_2:2, k_3:2, k_4:1\))で合成し、次の値を決定します。
$$
y_{n+1} = y_n + \frac{h}{6}(k_1 + 2k_2 + 2k_3 + k_4)
$$

なぜRK4は高精度なのか?
RK4は「一歩進む間の勾配の変化」を4回の関数評価でしっかり捉えるため、オイラー法よりも圧倒的に誤差が小さくなります。
特に、ステップ幅 \(h\) を半分にすると誤差が \(1/16\) になる「4次精度」を持ち、実用的なシミュレーションでは標準的な手法となっています。
また、計算コストはオイラー法の約4倍ですが、精度向上によって必要なステップ数が大幅に減るため、実質的な効率は非常に高いです。
4. 高階連立微分方程式への拡張
物理学の基本であるニュートンの運動方程式 \(F = ma\) は、位置の「2階」微分方程式です。
$$\frac{d^2 x}{dt^2} = \frac{F}{m}$$
しかし、これまで紹介した手法は「1階」微分方程式を対象としています。ここで、変数変換という非常に重要なテクニックが登場します。
「速度 \(v = dx/dt\)」を新しい変数として導入することで、1つの2階微分方程式を、2つの1階微分方程式のセット(連立微分方程式)に書き換えるのです。
$$
\begin{cases}
\frac{dx}{dt} = v \\
\frac{dv}{dt} = \frac{F}{m}
\end{cases}
$$
これにより、どんなに複雑な高階微分方程式も、多変数の1階微分方程式としてルンゲ・クッタ法で解くことが可能になります。
5. PyTorchによる実践:物理現象のシミュレーション
それでは、バネに繋がれたおもりの運動(単振動)を例に、オイラー法とルンゲ・クッタ法の実装と比較を行ってみましょう。
import torch
import matplotlib.pyplot as plt
def harmonic_oscillator(t, state):
"""
単振動の微分方程式 (2階ODEを1階連立に変形したもの)
state = [position, velocity]
dx/dt = vå
dv/dt = -k/m * x (ここではk/m = 1とする)
"""
x, v = state[0], state[1]
dxdt = v
dvdt = -x
return torch.stack([dxdt, dvdt])
def solve_euler(f, t_span, y0, h):
"""オイラー法ソルバー"""
t = torch.arange(t_span[0], t_span[1], h)
y = torch.zeros((len(t), len(y0)))
y[0] = y0
for i in range(len(t) - 1):
y[i+1] = y[i] + h * f(t[i], y[i])
return t, y
def solve_rk4(f, t_span, y0, h):
"""4次ルンゲ・クッタ法ソルバー"""
t = torch.arange(t_span[0], t_span[1], h)
y = torch.zeros((len(t), len(y0)))
y[0] = y0
for i in range(len(t) - 1):
k1 = f(t[i], y[i])
k2 = f(t[i] + h/2, y[i] + h/2 * k1)
k3 = f(t[i] + h/2, y[i] + h/2 * k2)
k4 = f(t[i] + h, y[i] + h * k3)
y[i+1] = y[i] + (h/6) * (k1 + 2*k2 + 2*k3 + k4)
return t, y
# 設定: 0秒から20秒まで、ステップ幅0.5 (意図的に大きく設定)
t_span = [0.0, 20.0]
y0 = torch.tensor([1.0, 0.0]) # 初期位置1, 初期速度0
h = 0.5
t_euler, y_euler = solve_euler(harmonic_oscillator, t_span, y0, h)
t_rk4, y_rk4 = solve_rk4(harmonic_oscillator, t_span, y0, h)
# 真の解 (cos(t))
t_fine = torch.linspace(0, 20, 200)
y_true = torch.cos(t_fine)
# 可視化
plt.figure(figsize=(12, 6))
plt.plot(t_fine.numpy(), y_true.numpy(), 'k--', label='True Solution (Analytic)', alpha=0.5)
plt.plot(t_euler.numpy(), y_euler[:, 0].numpy(), 'r-o', label='Euler Method', markersize=4)
plt.plot(t_rk4.numpy(), y_rk4[:, 0].numpy(), 'b-s', label='Runge-Kutta 4', markersize=4)
plt.title(f"Comparison of ODE Solvers (h={h})")
plt.xlabel("Time (t)")
plt.ylabel("Position (x)")
plt.legend()
plt.grid(True)
plt.show()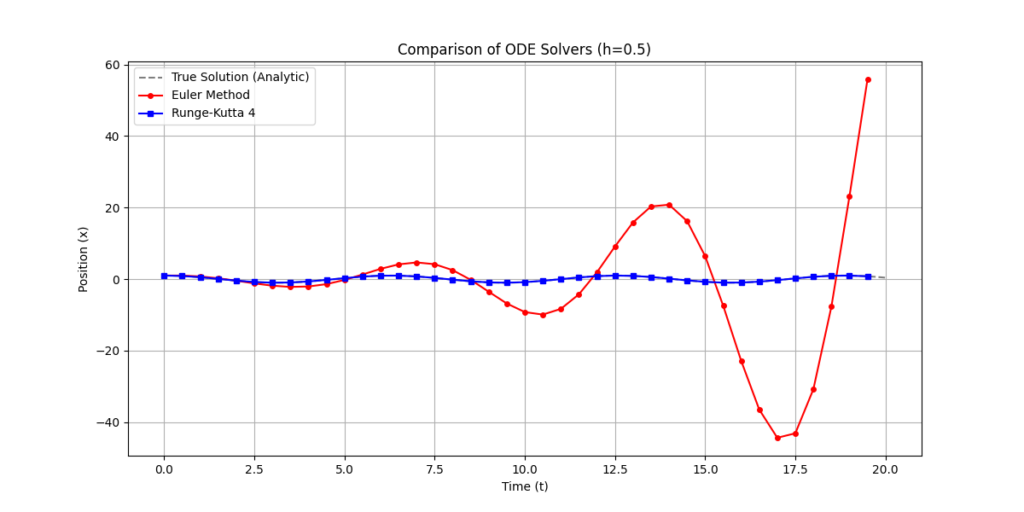
コードの解説
- 状態のベクトル化:
stateを[位置, 速度]というベクトルで扱うことで、単一の変数と同じようにルンゲ・クッタの公式を適用しています。 - 誤差の現れ方: グラフを見ると、オイラー法はステップが進むにつれて振幅がどんどん大きくなってしまっているのがわかります(エネルギーが不当に増加している)。一方、RK4は同じステップ幅でも真の解(点線)にほぼ完璧に重なっています。
- 計算コスト: RK4は1ステップあたり4回の関数評価が必要なため、オイラー法の4倍のコストがかかりますが、それ以上の圧倒的な精度向上が得られるため、実質的な効率はRK4の方が遥かに高いと言えます。
6. 誤差評価と歩み幅制御の考え方
実用的なODEソルバー(SciPyの solve_ivp など)では、ユーザーがステップ幅 \(h\) を指定するのではなく、「許容誤差(Tolerance)」を指定するのが一般的です。
ソルバーは、計算を行いながら「現在の \(h\) で誤差が許容範囲に収まっているか」を常にチェックします。
- 関数の変化が緩やかな場面: \(h\) を大きくして高速化。
- 激しい変化が起きる場面: \(h\) を極小にして精度を確保。
これを「適応型歩み幅制御(Adaptive Step Size Control)」と呼びます。有名な「Runge-Kutta-Fehlberg法(RKF45)」などは、4次と5次のルンゲ・クッタを同時に計算し、その差を誤差の推定値として利用するという賢い仕組みを持っています。
7. AIとの融合
最近のAI研究では、ニューラルネットワークの層を連続的な微分方程式として捉える Neural ODE が注目されています。
このモデルでは、ネットワークの順伝播がODEソルバーそのものになります。
# Neural ODE的な考え方の擬似コード
# z_next = z_now + ODE_Solver(NN_Module, z_now, dt)この時、ルンゲ・クッタ法のような高度なソルバーを微分可能な形で実装しておくことで、ソルバーの計算プロセスそのものを逆伝播(Backpropagation)させ、微分方程式の「形」そのものを学習させることが可能になります。
まとめ
第12回では、現象の未来を追うための「常微分方程式」の数値解法を学びました。
- 常微分方程式は、変化のルールから未来の挙動を導き出す道具である。
- オイラー法は基礎となるが、累積誤差が大きいため実用には注意が必要。
- ルンゲ・クッタ法(RK4)は、中間地点での勾配を利用する4次精度の手法で、シミュレーションの標準である。
- 変数変換により、高階の物理方程式も1階の連立方程式として統一的に扱える。
- 歩み幅制御は、精度と速度を両立させるための高度なテクニックである。
私たちが住む世界の物理法則は、微分方程式という美しい言語で書かれています。それをコードで解く力を身につけることは、現実世界の現象をデジタル空間に再現し、制御するための強力な一歩となります。
次回はいよいよ連載の最終回。空間的な広がりを持つ現象を記述する「偏微分方程式」と、それを解くための「線形反復法」について解説します。これまでの連載の集大成となる内容です。お楽しみに。
最後まで読んでいただきありがとうございます。
連載記事、各回へのリンク
Pythonで学ぶ数値計算のアルゴリズムと実装 第1回:多項式計算とテイラー展開 | アマチュア無線局JS2IIU
https://js2iiu.com/2025/12/31/python_numerical_01/
Pythonで学ぶ数値計算のアルゴリズムと実装 第2回:多項式補間とチェビシェフ補間の戦略 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/01/python_numerical_02/
Pythonで学ぶ数値計算のアルゴリズムと実装 第3回:積分の基礎:中点則、台形則からシンプソン則まで | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/01/python_numerical_03/
Pythonで学ぶ数値計算のアルゴリズムと実装 第4回:高度な数値積分:二重指数型(DE)公式と広義積分 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/01/python_numerical_04/
Pythonで学ぶ数値計算のアルゴリズムと実装 第5回:計算の「正しさ」を評価する:ノルムと条件数 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/01/python_numeric_05/
Pythonで学ぶ数値計算のアルゴリズムと実装 第6回:連立一次方程式の直截解法:ガウス消去法とピボット選択 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/01/python_numerical_06/
Pythonで学ぶ数値計算のアルゴリズムと実装 第8回:スパース性を活かす:帯行列の高速計算アルゴリズム | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/02/python_numerical_08/
Pythonで学ぶ数値計算のアルゴリズムと実装 第9回:最小二乗法とQR分解:ハウスホルダー変換による安定化 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/02/python_numerial_09/
Pythonで学ぶ数値計算のアルゴリズムと実装 第10回:非線形方程式の探索:2分法からニュートン法まで | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/03/python_numerical_10/
Pythonで学ぶ数値計算のアルゴリズムと実装 第11回:行列の本質を捉える:固有値問題の数値解法 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/03/python_numerical_11/
Pythonで学ぶ数値計算のアルゴリズムと実装 第12回:現象の変化を追う:ルンゲ・クッタ法による常微分方程式の解法 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/03/python_numerical_12/
Pythonで学ぶ数値計算のアルゴリズムと実装 第13回:空間の熱と振動を解く:偏微分方程式の差分近似と反復解法 | アマチュア無線局JS2IIU
https://js2iiu.com/2026/01/03/python_numerical_13/



コメント