こんにちは、JS2IIUです。
プログラミングと物理シミュレーションの世界へようこそ。本連載では、Pythonを武器に、複雑で美しい流体の動きを解き明かす「数値流体力学(CFD: Computational Fluid Dynamics)」の世界を覗いてみます。
近年、AI技術、特にディープラーニングの世界でも、物理法則をニューラルネットワークに組み込む「Physics-Informed Neural Networks (PINNs)」などの登場により、物理シミュレーションの知識はデータサイエンティストやエンジニアにとっても避けては通れない非常に重要な領域となっています。
第1回となる今回は、流体力学の最も根幹をなす概念である「質量保存則」と、それを数式で表した「連続の式」について学びます。難解な数式をただ眺めるのではなく、Pythonでの実装を通じて、流体の動きを「領域」で捉える感覚を身につけていきましょう。今回もよろしくお願いします。
1. 流体をどう捉えるか? ― ラグランジュ的視点とオイラー的視点
流体の動きを計算・記述する際、まず最初に考えるべきは「流体をどのように捉えるか?」という視点の選択です。これには大きく分けて2つのアプローチがあります。
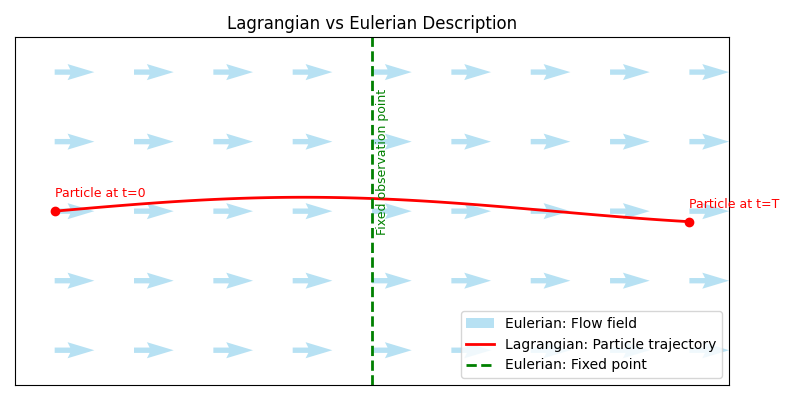
ラグランジュ的視点 (Lagrangian Description)
ラグランジュ的視点では、流体を構成する無数の「粒子」や「微小な要素」に注目し、それぞれの粒子が時間とともにどのように動くかを追跡します。たとえば、ビリヤードの球や水中に浮かべた小さな葉っぱを一つひとつ追いかけるイメージです。
この方法では、各粒子の位置や速度、加速度などを時間発展させていきます。粒子法(SPH: Smoothed Particle Hydrodynamics)や分子動力学法などがこの考え方に基づいています。
メリット:
- 各粒子の履歴や経路が自然に得られるため、混合や拡散、界面の追跡などに強い。
- 物質の移動や変形を直感的に理解しやすい。
デメリット:
- 粒子数が多い場合、計算コストが非常に高くなる。
- 境界条件の扱いが難しい場合がある。
オイラー的視点 (Eulerian Description)
一方、オイラー的視点では、空間上に固定された「領域(コントロールボリューム)」を設定し、その中を流体がどのように通過していくかを観察します。たとえば、川の橋の上から、同じ場所を流れていく水の流れや速さ、密度の変化を観察するイメージです。
この方法では、空間の各点(格子点)における流体の物理量(速度、密度、圧力など)が時間とともにどう変化するかを記述します。多くの数値流体力学(CFD)手法や有限差分法・有限体積法はこの視点を採用しています。
メリット:
- 固定格子上で計算するため、計算効率が高く、大規模な流れの解析に向いている。
- 境界条件の設定や外部からの流入・流出の管理がしやすい。
デメリット:
- 粒子の追跡や混合の詳細な挙動を直接得るのは難しい。
- 格子の分解能に依存し、細かい現象の表現には高解像度が必要。
このように、ラグランジュ的視点は「粒子を追う」、オイラー的視点は「場所に注目する」という違いがあります。
数値流体力学の多くの場面では、計算効率や実装の容易さから後者のオイラー的視点が主流です。
今回のテーマである「連続の式」も、このオイラー的視点に基づいた「コントロールボリューム」の考え方から導き出されます。
2. コントロールボリュームと質量保存則
「質量保存則」とは、非常にシンプルな法則です。「ある空間内に存在する物質の量の変化は、その空間に入ってきた量と出ていった量の差に等しい」というものです。
例えば、ある立方体の箱(これをコントロールボリュームと呼びます)を想像してください。
- 箱の中に水が流れ込みます。
- 同時に、箱から水が流れ出します。
- もし「入る量 > 出る量」であれば、箱の中の水の量は増えます。
- もし「入る量 < 出る量」であれば、箱の中の水の量は減ります。
この当たり前とも思える関係を、流体の密度 \(\rho\) と速度ベクトル \(\mathbf{u} = (u, v, w)\) を使って数学的に表現したものが「連続の式」です。
連続の式の微分形式
連続の式(continuity equation)は、流体の「質量保存則」を数学的に表現したものです。流体がどんなに動いても、全体の質量は保存される――この当たり前の原理が、流体力学の根幹となっています。
微分形式の式
一般的な流体(圧縮性も考慮)における連続の式は、次のように書かれます:
$$
\frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \mathbf{u}) = 0
$$
ここで、
- \(\rho\) は流体の密度(kg/m³)
- \(\mathbf{u}\) は速度ベクトル(m/s)
この式は「ある場所の密度の変化」と「その場所から出入りする質量の流れ」のバランスを表しています。
各項の物理的意味
- \(\frac{\partial \rho}{\partial t}\):
- ある固定した点(オイラー的視点)で、密度が時間とともにどれだけ変化しているかを表します。
- 例:水たまりの水位が時間とともに上がったり下がったりするイメージ。
- \(\nabla \cdot (\rho \mathbf{u})\):
- 「ダイバージェンス(発散)」と呼ばれる演算子で、単位体積・単位時間あたりにその点からどれだけの質量が外へ出ていくか(または入ってくるか)を示します。
- 例:スポンジの中の水が外へ染み出していく様子や、逆に外から流れ込む様子。
直感的なイメージ
この式は、
- もし密度が増えている(\(\frac{\partial \rho}{\partial t} > 0\))なら、その分だけ周囲から流体が流れ込んでいる(\(\nabla \cdot (\rho \mathbf{u}) < 0\))はず。
- 逆に、密度が減っているなら、流体が外へ流れ出している。
つまり「入る量−出る量=中身の増減」という、質量保存の原理そのものです。
例えば、密閉された部屋に空気が流れ込む場合、部屋の中の空気の密度は増えます。逆に、窓を開けて空気が外へ出ていけば、密度は減ります。連続の式は、こうした現象を数式で厳密に記述するための道具です。
数学的な導出の背景
この式は、コントロールボリューム(任意の空間領域)に対して「出入りする質量の流量」と「内部の質量変化」をバランスさせることで導かれます。積分形から微分形への変換(ガウスの発散定理)を経て、上記の微分形式が得られます。
非圧縮性流体の場合
非圧縮性流体(incompressible fluid)とは、圧力を加えても密度 \(\rho\) がほとんど変化しない流体のことです。水や油、空気(低速・低圧の場合)などが代表例です。
物理的な意味
圧縮性流体では、流れの中で密度が変化しますが、非圧縮性流体では「どこでも密度は一定」とみなせます。つまり、流体がどれだけ動いても、体積あたりの質量は変わりません。
数式の変化
連続の式の微分形式
\(\frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \mathbf{u}) = 0\)
で、\(\rho\) が一定(時間・空間で変化しない)とすると、\(\frac{\partial \rho}{\partial t} = 0\) かつ \(\rho\) を外に出せるので、
\(\nabla \cdot \mathbf{u} = 0\)
という非常にシンプルな式になります。
「ある領域に流体が入った分だけ、必ず同じ量が外へ出ていく」――つまり、流体の体積がどこでも保存されるということです。水道管や川の流れなど、日常の多くの流体現象はこの条件を満たしています。
シミュレーションでの重要性
数値流体力学(CFD)では、非圧縮性条件 \(\nabla \cdot \mathbf{u} = 0\) を満たすように速度場や圧力場を調整することが計算の中心となります。もしこの条件が破綻すると、質量保存が守られず、シミュレーション結果が物理的に意味を持たなくなります。
現実の例
- 水道管の中の水
- プールの水
- ゆっくり流れる空気(音速より十分遅い場合)
これらは、流れの中で密度変化が無視できるため、非圧縮性流体として扱われます。
3. Pythonによる実装:離散化と質量のバランス計算
概念を理解したところで、実際にPythonコードを書いて、格子状に区切られた空間で質量保存がどのように計算されるかを確認してみましょう。
今回は、2次元の格子(グリッド)を定義し、各格子点での流出入バランス(ダイバージェンス)を計算します。PyTorchを利用することで、将来的なAIモデルへの統合も見据えたテンソル計算を行います。
シミュレーション設定
- 2次元の計算領域をメッシュ(格子)に分割します。
- 各格子点に速度ベクトル \((u, v)\) を与えます。
- 中央の領域から外側へ広がるような流れを作り、ダイバージェンスを計算します。
import torch
import matplotlib.pyplot as plt
def calculate_divergence_2d(u, v, dx, dy):
"""
2次元速度場(u, v)のダイバージェンスを計算する。
Args:
u (torch.Tensor): x方向の速度成分 (Ny, Nx)
v (torch.Tensor): y方向の速度成分 (Ny, Nx)
dx (float): x方向の格子間隔
dy (float): y方向の格子間隔
Returns:
torch.Tensor: ダイバージェンス (Ny-2, Nx-2)
"""
# 中央差分法を用いて勾配を近似計算する
# du/dx = (u[i, j+1] - u[i, j-1]) / (2 * dx)
# dv/dy = (v[i+1, j] - v[i-1, j]) / (2 * dy)
du_dx = (u[1:-1, 2:] - u[1:-1, :-2]) / (2 * dx)
dv_dy = (v[2:, 1:-1] - v[:-2, 1:-1]) / (2 * dy)
divergence = du_dx + dv_dy
return divergence
# --- パラメータ設定 ---
nx, ny = 50, 50 # 格子数
lx, ly = 1.0, 1.0 # 領域のサイズ
dx = lx / (nx - 1)
dy = ly / (ny - 1)
# 座標系の作成
x = torch.linspace(0, lx, nx)
y = torch.linspace(0, ly, ny)
Y, X = torch.meshgrid(y, x, indexing='ij')
# --- 速度場の定義 ---
# 例として、中心(0.5, 0.5)から放射状に広がる流れを作る
# この流れは中心で「湧き出し」があるため、ダイバージェンスが正になるはず
u = (X - 0.5) * torch.exp(-((X - 0.5)**2 + (Y - 0.5)**2) * 20)
v = (Y - 0.5) * torch.exp(-((X - 0.5)**2 + (Y - 0.5)**2) * 20)
# ダイバージェンスの計算
div = calculate_divergence_2d(u, v, dx, dy)
# --- 可視化 ---
plt.figure(figsize=(12, 5))
# 速度場のベクトル表示 (Quiver plot)
plt.subplot(1, 2, 1)
plt.quiver(X[::3, ::3], Y[::3, ::3], u[::3, ::3], v[::3, ::3])
plt.title("Velocity Field (Radial Flow)")
plt.xlabel("x")
plt.ylabel("y")
# ダイバージェンスのカラーマップ表示
plt.subplot(1, 2, 2)
im = plt.imshow(div, extent=[dx, lx-dx, dy, ly-dy], origin='lower', cmap='RdBu_r')
plt.colorbar(im, label='Divergence (mass flux balance)')
plt.title("Calculated Divergence")
plt.xlabel("x")
plt.ylabel("y")
plt.tight_layout()
plt.show()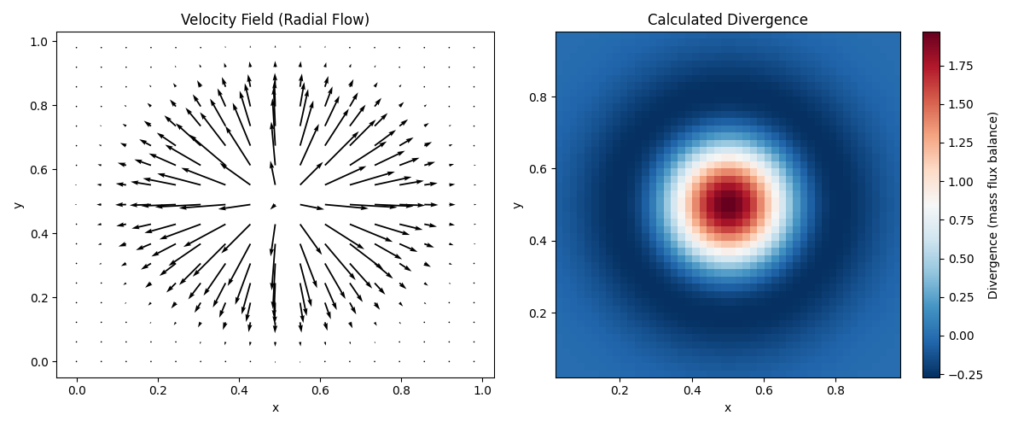
コードの解説
- 中央差分法による近似:
数式上の微分 \(\frac{\partial u}{\partial x}\) を、コンピュータで扱うために「隣り合う格子点の値の差」で近似しています。具体的には(u[右] - u[左]) / (2 * 間隔)という計算を行っています。これが数値シミュレーションにおける「離散化」の第一歩です。 - スライシングによる効率化:
PyTorch(やNumPy)の強力な機能であるスライシングu[1:-1, 2:]を使うことで、forループを使わずに格子全体を一括で計算しています。これは計算速度を劇的に向上させるための鉄則です。 - ダイバージェンスの意味:
出力されたグラフの右側を見てください。中心付近が赤く(正の値)なっていることがわかります。これは「この点から流体が外へ湧き出している」ことを意味します。質量保存則の観点から言えば、もしここが非圧縮性流体であれば、このような「湧き出し」は本来許されません。実際のシミュレーションでは、このダイバージェンスをゼロに抑えるように圧力を調整していくことになります。
4. 実践的な視点:なぜ「連続の式」が重要なのか?
流体シミュレーションやAIによる物理モデリングを行う際、「連続の式(質量保存則)」は極めて重要な役割を果たします。
シミュレーションの安定性と物理的妥当性
数値流体力学(CFD)や物理シミュレーションでは、計算が進むうちに値が「爆発(無限大に発散)」したり、現実にはあり得ない流れが生じることがあります。その多くは、質量保存(連続の式)が局所的に破綻していることが原因です。
例えば、ある領域で「入る量」と「出る量」のバランスが崩れると、そこに質量が“湧いたり消えたり”することになり、物理的に不自然な現象が発生します。これを防ぐためには、連続の式を厳密に守ることが不可欠です。
AI・ディープラーニング応用での意義
近年は、ディープラーニングを用いた流体解析(PINNs: Physics-Informed Neural Networks)などでも、連続の式の重要性が増しています。ニューラルネットワークが出力する速度場が「連続の式」を満たすように、損失関数(Loss Function)に物理制約項を加えるのが一般的です。
$$
Loss_{physics} = | \nabla \cdot \mathbf{u} |^2
$$
この項を加えることで、データが少ない領域や未知の状況でも、物理的に妥当な予測ができるようになります。つまり「物理法則を知っているAI」を作るための鍵が連続の式なのです。
現実の現象と保存則の意義
自然界の流体現象は、必ず質量保存則(連続の式)に従っています。たとえば、川の流れ、空気の循環、海流、パイプ内の水の流れなど、どんなスケールでも「入った分だけ必ず出る」ことが守られています。
この保存則を破ると、計算上は一見うまくいっているように見えても、実際には全く現実と異なる結果になってしまいます。
このように、連続の式は「物理的に正しい流体現象」を再現するための絶対的なルールであり、数値計算・AI応用の両面で不可欠な基礎となっています。
5. まとめと次回の予告
今回は、流体力学の第一歩として以下の内容を学びました。
- 流体を空間上の固定領域で捉えるオイラー的視点。
- 「入る量と出る量の差が内部の蓄積量に等しい」という質量保存則。
- それを数式化した連続の式。
- PythonとPyTorchを用いた、格子点上でのダイバージェンス(湧き出し)の計算方法。
流体が「質量を保ちながら動く」というルールを理解した今、次は「流体はどうやって動かされるのか?」という疑問が湧いてくるはずです。
次回、第2回では、ニュートンの運動法則を流体に適用した「運動量保存則」と、熱の変化を司る「エネルギー保存則」について詳しく解説します。流体に働く「力」の正体に迫っていきましょう。
プログラミングを通じて物理を理解する楽しさを、ぜひこの連載を通じて体感してください。
最後まで読んでいただきありがとうございます。



コメント