こんにちは、JS2IIUです。
前回の第1回では、流体力学の最も基本的なルールである「質量保存則」と、それを数式化した「連続の式」について学びました。流体がいかに形を変えようとも、その質量が勝手に消えたり増えたりすることはない、という当たり前ながらも強力な制約を、コントロールボリューム(固定された領域)の視点から理解しました。
しかし、質量が保存されるだけでは流体は動きません。流体が加速したり、曲がったり、あるいは熱を持って膨張したりするのはなぜでしょうか。第2回となる今回は、流体の「動き」と「熱の状態」を支配する2つの重要な物理法則、運動量保存則とエネルギー保存則について掘り下げていきます。今回もよろしくお願いします、
1. 運動量保存則:流体におけるニュートンの第2法則
高校物理で学んだ「ニュートンの運動方程式(\(F = ma\))」を覚えているでしょうか。運動量保存則は、この法則を流体という連続体に適用したものです。
運動量(質量 \(\times\) 速度)の変化は、その流体に加わる力の合計に等しい、という考え方です。流体における「力」には、大きく分けて2つの種類があります。
- 表面力 (Surface Forces):
コントロールボリュームの表面を介して働く力です。代表的なものは「圧力」です。また、後の回で詳しく扱う「粘性(摩擦力)」も表面力に含まれます。 - 外力 (Body Forces):
流体の体積全体に直接働く力です。最も身近な例は「重力」です。
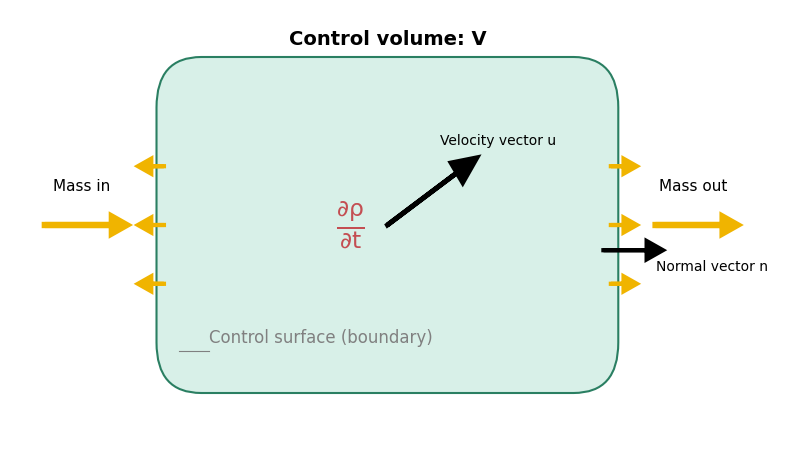
運動量方程式のイメージ
コントロールボリューム内の運動量の変化を数式で表すと、以下のようになります。
この式の各項を直感的に解釈してみましょう。
- 第1項 \(\frac{\partial (\rho \mathbf{u})}{\partial t}\): ある地点での運動量の時間変化。
- 第2項 \(\nabla \cdot (\rho \mathbf{u} \otimes \mathbf{u})\): 移流項。流体そのものの流れによって、運動量が隣の領域へ運ばれていく効果を表します。流体力学を難しく、かつ面白くしている「非線形性」の源泉です。
- 右辺: 圧力勾配や重力など、流体を加速させる原因となる力。
簡単に言えば、「ある場所の流体の速度が変わるのは、力が働いたからか、あるいは別の速度を持った流体が流れ込んできたからだ」と言っているのです。
2. エネルギー保存則:熱と仕事のバランス
流体が高速で動く場合や、温度変化が激しい現象を扱う場合、質量保存則や運動量保存則だけでは現象を十分に記述できません。ここで重要になるのが、エネルギー保存則です。これは熱力学第一法則に基づいており、流体力学においては「コントロールボリューム(観測対象領域)内のエネルギーの総量変化は、外部から加えられた熱量と、外部に対して行った仕事の和に等しい」という形で表現されます。
エネルギー保存則の本質は、「エネルギーは形を変えても失われない」という普遍的な原理です。流体の場合、エネルギーは主に以下の3つの形で存在します。
- 内部エネルギー: 分子の熱運動や分子間力によるエネルギー。温度変化や相変化(蒸発・凝縮など)に深く関わります。
- 運動エネルギー: 流体全体のマクロな運動(流れや回転など)によるエネルギー。(\frac{1}{2}\rho u^2) のような形で表されます。
- 位置エネルギー(ポテンシャルエネルギー): 重力場など外力場に対する位置によるエネルギー。高低差のある流れや落下運動などで重要です。
これらのエネルギーは、流体の中で相互に変換されることがあります。たとえば、流れが速くなると運動エネルギーが増え、圧縮や膨張によって内部エネルギーが変化し、また高い場所から低い場所へ流れると位置エネルギーが運動エネルギーに変換されます。
エネルギー保存則を数式で表すと、次のようになります。
$$
\frac{\partial}{\partial t}(\text{エネルギー密度}) + \nabla \cdot (\text{エネルギー流束}) = \text{外部からの熱供給} + \text{外部への仕事}
$$
ここで「エネルギー密度」は単位体積あたりの全エネルギー(内部エネルギー+運動エネルギー+位置エネルギー)を指し、「エネルギー流束」は流体の運動や熱伝導によってエネルギーが運ばれる量を表します。
熱と仕事のバランス
エネルギー保存則の右辺には「熱」と「仕事」が登場します。
- 熱(Heat): 流体に外部から加えられる熱量。たとえば、加熱器で温めたり、化学反応で発生した熱などが該当します。熱は主に分子のランダムな運動(内部エネルギー)として流体に蓄えられます。
- 仕事(Work): 流体が外部に対して行う、または外部から受ける力学的な仕事。たとえば、ピストンで圧縮されたり、流体がタービンを回すときなどです。仕事は運動エネルギーや位置エネルギーの変化として現れます。
このように、流体のエネルギーは「熱」と「仕事」のやりとりによって増減し、またエネルギーの形態も相互に変換されます。
どんなときに重要か?
エネルギー保存則は、特に以下のような現象で不可欠です。
- 燃焼や化学反応を伴う流れ: 発熱・吸熱反応による温度変化や、生成物のエネルギー変化を正確に記述する必要があります。
- 超音速・高温の流れ: 航空機の周りの空気やロケット噴射など、運動エネルギーと内部エネルギーの変換が激しい現象。
- 圧縮性流体: 空気やガスの圧縮・膨張を伴う流れでは、温度や圧力の変化が密接に関係します。
一方で、日常的な水や低速の空気の流れ(非圧縮性流体)では、温度変化やエネルギーのやりとりが流れの運動に与える影響が小さいため、エネルギー保存則を省略できる場合も多いです。そのため、流体力学の入門ではまず運動量保存則や質量保存則を中心に学び、より複雑な現象を扱う際にエネルギー保存則を導入するのが一般的です。
このように、エネルギー保存則は「流体の熱的・力学的なふるまい」を統合的に理解するための強力なツールです。自分が扱う現象で「熱」や「圧縮性」が重要かどうかを見極め、必要に応じてエネルギー保存則を適用することが、流体力学の実践では大切になります。
3. バロトロピー流という重要な仮定
流体の計算をシンプルにするために、しばしば導入されるのがバロトロピー流 (Barotropic Flow) という概念です。このセクションでは、この重要な仮定について詳しく見ていきましょう。
3.1 バロトロピー流の定義
通常、流体の密度 \(\rho\) は圧力 \(P\) と温度 \(T\) の両方に依存します。理想気体を例に取ると、状態方程式は次のように表されます。
$$
P = \rho RT
$$
ここで、\(R\) は気体定数です。この式からわかるように、密度を知るためには圧力と温度の両方の情報が必要になります。
しかし、バロトロピー流では、「密度は圧力のみの関数である」と仮定します。
$$
\rho = f(P)
$$
この仮定の下では、ある圧力値が決まれば、温度の情報がなくても密度が一意に決定されます。言い換えれば、等圧面(圧力が一定の面)と等密度面(密度が一定の面)が常に一致している状態を意味します。
3.2 なぜこの仮定が重要なのか?
バロトロピー流の仮定が重要な理由は、計算の自由度を大幅に減らせることにあります。
通常の流体計算では、以下の3つの保存則を全て解く必要があります。
- 質量保存則(連続の式)
- 運動量保存則(ナビエ・ストークス方程式など)
- エネルギー保存則(熱力学第一法則)
これらに加えて、圧力・密度・温度を結びつける状態方程式も必要です。未知数が多く、計算コストも非常に高くなります。
しかし、バロトロピー流の仮定を導入すると、密度 \(\rho\) と圧力 \(P\) の関係が \(\rho = f(P)\) で直接表されるため、エネルギー保存則を解く必要がなくなります。つまり、
- 質量保存則(連続の式)で密度の時間発展を追う
- 運動量保存則で速度と圧力を求める
- 状態方程式 \(\rho = f(P)\) で密度と圧力を結びつける
という3つのステップだけで、流体の挙動を完全に記述できるのです。これは、特に大規模な数値シミュレーションにおいて計算時間とメモリの大幅な削減につながります。
3.3 バロトロピー流が成立する条件
では、どのような状況でバロトロピー流の仮定が妥当なのでしょうか?主な条件は以下の通りです。
(1) 等温流れ(Isothermal Flow)
流体全体の温度が一定に保たれている場合、密度は圧力のみの関数になります。理想気体の場合、\(T = \text{const}\) とすると、
$$
\rho = \frac{P}{RT} = \text{const} \times P
$$
となり、\(\rho \propto P\) の線形関係が成り立ちます。
(2) 断熱流れ(Isentropic Flow)
エントロピーが一定に保たれる理想的な流れ(摩擦がなく、熱の出入りもない)では、圧力と密度の間に以下のポリトロープ関係が成立します。
$$
P = K \rho^\gamma
$$
ここで、\(\gamma\) は比熱比(通常、空気では約1.4)、\(K\) は定数です。この関係も \(\rho = f(P)\) の形に変形でき、バロトロピー流として扱えます。
(3) 非圧縮性流体
液体のように、密度がほとんど変化しない流体(\(\rho = \text{const}\))も、広い意味でバロトロピー流の一種と見なせます。この場合、密度が圧力に依存しないため、最もシンプルな形になります。
3.4 バロクリニック流との対比
バロトロピー流の反対概念として、バロクリニック流 (Baroclinic Flow) があります。バロクリニック流では、等圧面と等密度面が交差します。つまり、温度分布が複雑で、同じ圧力でも場所によって密度が異なる状態です。
典型的な例は、前線を伴う気象現象です。暖気と寒気がぶつかり合う前線では、同じ高度(同じ圧力)でも温度が大きく異なるため、密度も異なります。このような現象では、エネルギー保存則を含めた完全な方程式系を解く必要があります。
3.5 バロトロピー流の実際の応用例
バロトロピー流の仮定は、以下のような場面で広く利用されています。
- 音波の伝播: 音波は微小な圧力変動として伝わりますが、その変化は非常に速く、熱の伝達が追いつかないため、断熱的(エントロピー一定)な過程と見なせます。このため、バロトロピー流として扱えます。
- 水中の流れ: 水は非圧縮性流体として良い近似ができるため、密度を一定(\(\rho = \text{const}\))とするバロトロピー流として扱われます。
- 大気の大規模運動: 気象学の順圧モデル (Barotropic Model) では、大気の鉛直方向の温度構造を無視し、水平方向の運動のみに着目します。これにより、高気圧・低気圧の大まかな動きを効率的に計算できます。
3.6 まとめ:バロトロピー流の利点と限界
利点:
- エネルギー保存則を解く必要がないため、計算コストが大幅に削減される。
- 数学的にシンプルで、解析的な解が得られる場合もある。
限界:
- 温度変化が重要な現象(燃焼、対流、前線など)には適用できない。
- 実際の流れは多くの場合バロクリニックであり、バロトロピー流は理想化された近似に過ぎない。
自分が扱う問題が「温度の影響を無視できるか」「断熱的か等温的か」といった視点から、バロトロピー流の仮定が妥当かどうかを見極めることが、流体力学の実践において重要です。
4. Pythonによる実装:圧力勾配による流体の加速
運動量保存則の最も本質的な部分である「圧力の差(圧力勾配)によって流体が加速される」様子をPythonでシミュレーションしてみましょう。
今回は、静止している流体に対して、局所的に高い圧力を与えたとき、速度場がどのように変化するかを計算します。ここでも、効率的な配列演算のためにPyTorchを使用します。
アルゴリズムの概要
- 静止した速度場 \((u, v) = 0\) を用意する。
- 中心に高圧、周囲に低圧の圧力場 \(P\) を定義する。
- 運動量方程式の一部(圧力勾配項)のみを取り出し、速度を更新する。
$$ \frac{\partial \mathbf{u}}{\partial t} \approx – \frac{1}{\rho} \nabla P $$
import torch
import matplotlib.pyplot as plt
def update_velocity_by_pressure(u, v, p, dx, dy, dt, rho):
"""
圧力勾配に基づいて速度場を更新する(運動量保存則の一部)
Args:
u, v (torch.Tensor): 現在の速度成分
p (torch.Tensor): 圧力場
dx, dy (float): 格子間隔
dt (float): タイムステップ
rho (float): 密度
Returns:
u_new, v_new (torch.Tensor): 更新後の速度成分
"""
# 速度場をコピー
u_new = u.clone()
v_new = v.clone()
# 内部の格子点に対して圧力勾配を計算 (中央差分)
# du/dt = - (1/rho) * dp/dx
# dv/dt = - (1/rho) * dp/dy
dp_dx = (p[1:-1, 2:] - p[1:-1, :-2]) / (2 * dx)
dp_dy = (p[2:, 1:-1] - p[:-2, 1:-1]) / (2 * dy)
# 速度の更新 (オイラー法)
u_new[1:-1, 1:-1] -= dt * (1.0 / rho) * dp_dx
v_new[1:-1, 1:-1] -= dt * (1.0 / rho) * dp_dy
return u_new, v_new
# --- パラメータ設定 ---
nx, ny = 40, 40
lx, ly = 1.0, 1.0
dx, dy = lx / (nx - 1), ly / (ny - 1)
dt = 0.01 # 時間刻み
rho = 1.0 # 密度(一定と仮定)
# 座標系の作成
x = torch.linspace(0, lx, nx)
y = torch.linspace(0, ly, ny)
Y, X = torch.meshgrid(y, x, indexing='ij')
# --- 初期状態の定義 ---
u = torch.zeros((ny, nx))
v = torch.zeros((ny, nx))
# 圧力場: 中心に高い圧力を配置 (ガウス分布)
p = torch.exp(-((X - 0.5)**2 + (Y - 0.5)**2) * 20)
# --- 時間発展の計算 (10ステップ分) ---
u_step, v_step = u, v
for _ in range(10):
u_step, v_step = update_velocity_by_pressure(u_step, v_step, p, dx, dy, dt, rho)
# --- 可視化 ---
plt.figure(figsize=(12, 5))
# 圧力場の表示
plt.subplot(1, 2, 1)
plt.contourf(X, Y, p, cmap='viridis')
plt.colorbar(label='Pressure')
plt.title("Initial Pressure Field")
plt.xlabel("x")
plt.ylabel("y")
# 加速された速度場の表示
plt.subplot(1, 2, 2)
plt.quiver(X[::2, ::2], Y[::2, ::2], u_step[::2, ::2], v_step[::2, ::2])
plt.title("Velocity after Acceleration (Momentum)")
plt.xlabel("x")
plt.ylabel("y")
plt.tight_layout()
plt.show()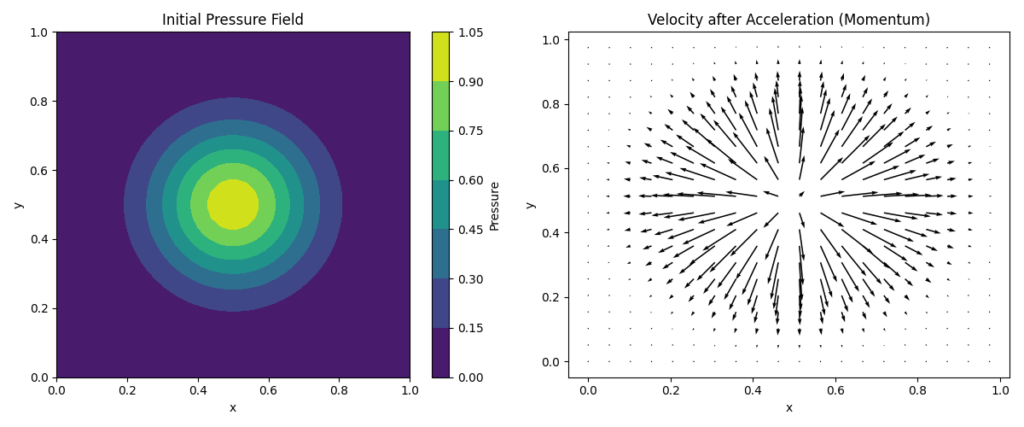
コードの解説
- 圧力勾配の計算:
dp_dx = (p[1:-1, 2:] - p[1:-1, :-2]) / (2 * dx)というコードは、ある点において「右側の圧力と左側の圧力の差」を見ています。圧力が高い方から低い方へと流体を押し出す力が働くため、速度の更新時にはマイナス記号u_new -= ...がついています。 - 速度の更新:
ここでは加速度 \(a = \frac{F}{m}\) の考え方に基づき、短い時間dtの間にどれだけ速度が変化するかを計算しています。これは数値積分の最もシンプルな形である「前進オイラー法」です。 - 結果の解釈:
右側のグラフを見てください。中心の高圧部から、外側の低圧部に向かって放射状に矢印(速度ベクトル)が伸びているのがわかります。これが、運動量保存則に従って流体が力を受け、加速した結果です。
5. なぜ「エネルギー保存」はあまり出てこないの?
初心者の方が流体力学を学び始めると、「連続の式」と「ナビエ・ストークス方程式(運動量保存)」ばかりが出てきて、エネルギー保存則が脇に追いやられているように感じることがあるかもしれません。
その理由は、私たちが日常的に扱う「水」や「ゆっくり流れる空気」において、エネルギーの変化が速度や圧力に与える影響が極めて小さいからです。これらは「非圧縮性流体」としてモデル化され、温度変化が流れを駆動しない(自然対流などを除く)限り、エネルギー保存則を解かずに計算を完結できるのです。
しかし、航空宇宙工学のように音速を超える流れを扱う場合や、エンジン内部の燃焼をシミュレーションする場合は、エネルギー保存則が主役になります。自分が解きたい問題が「熱」や「圧縮性」を無視できるかどうかを判断することが、エンジニアとしての第一歩です。
6. まとめと次回の予告
第2回では、流体の動的な側面を司る法則について学びました。
- 流体の加速と移流を記述する運動量保存則。
- 熱と仕事のバランスを保つエネルギー保存則。
- 密度と圧力を直接結びつける便利な仮定であるバロトロピー流。
- Pythonを用いて、圧力勾配が速度場を生み出すプロセスを実装。
これで、流体を支配する「3つの保存則(質量・運動量・エネルギー)」が出揃いました。これらはいわば、流体という世界の憲法です。
次回、第3回では、これらの法則を「粘性のない理想的な流体」に適用したオイラーの運動方程式を詳しく見ていきます。美しい「ポテンシャル流」の世界を通じて、流体の形を数学的に捉える方法を学んでいきましょう。
最後まで読んでいただきありがとうございます。



コメント