こんにちは、JS2IIUです。。Pythonで攻略する流体力学シミュレーション連載の第4回です。
前回は、摩擦のない理想的な「完全流体」を扱い、オイラーの運動方程式やポテンシャル流れの美しさを学びました。しかし、最後に触れた「ダランベールのパラドックス」が示す通り、理想化しすぎたモデルでは現実の空気抵抗や「ドロドロとした粘り気」を説明することができません。
今回はいよいよ、流体力学の核心であり、現代物理学・工学における最重要方程式のひとつである「ナビエ・ストークス方程式(Navier-Stokes equations)」に挑みます。現実の流体が持つ「粘性」を数式でどう表現し、それが流れにどのような影響を与えるのかを解き明かしていきましょう。
1. 粘性流体:流体の「粘り気」の正体
現実の流体(水、空気、オイルなど)には、必ず「粘り気」が存在します。これを物理学では粘性(Viscosity)と呼び、流体の運動において極めて重要な役割を果たします。
粘性とは、流体内部で隣り合う層同士が相対運動(速度差)を持つときに、その運動を妨げる摩擦的な力が発生する性質です。例えば、ハチミツと水を比較すると、ハチミツはスプーンですくって垂らすとゆっくりと糸を引くように流れますが、水はさらさらと速く流れます。この違いは、ハチミツの方が粘性が高い(内部摩擦が強い)ためです。
技術的には、粘性は「隣接する流体層間に働くせん断応力(摩擦力)」として定義されます。流体が流れるとき、速い層は隣の遅い層を引きずり、逆に遅い層は速い層の動きを妨げます。このとき、運動量が層間でやり取りされることで、速度のムラが徐々に均されていきます。この運動量の交換を担う内力が「粘性応力(viscous stress)」です。
分子レベルで見ると、流体分子は熱運動によって絶えず移動しており、速い層から遅い層へ、またはその逆へと分子が飛び出すことで運動量が伝達されます。これがマクロなスケールで「粘性」として観測される現象の本質です。気体では分子の衝突による運動量輸送、液体では分子間力による粘性が支配的です。
粘性の効果は、流体の種類や温度によって大きく異なります。例えば、空気や水のような低粘性流体では、流れが速く滑らかですが、オイルやハチミツのような高粘性流体では、流れが遅く、形状を保ちやすくなります。工学的には、配管内の圧力損失や、機械部品の潤滑、気象現象、さらには生体内の血流など、粘性の影響は極めて広範囲に及びます。
粘性係数とニュートンの粘性法則
多くの場合、この摩擦の強さは速度の勾配(場所による速度の差)に比例します。これを「ニュートンの粘性法則」と呼び、比例定数を粘性係数(\(\mu\))と呼びます。
$$
\tau = \mu \frac{\partial u}{\partial y}
$$
ここで \(\tau\)(タウ)はせん断応力です。この \(\mu\) が大きいほど、ドロドロとした「粘り強い」流体であることを意味します。
2. ナビエ・ストークス方程式の導出
前回紹介したオイラー方程式は、粘性(内部摩擦)が無視できる理想流体の運動を記述するものでした。しかし、現実の流体では粘性の効果が無視できないため、より一般的な運動方程式が必要です。ここで登場するのがナビエ・ストークス(Navier-Stokes, NS)方程式です。
ナビエ・ストークス方程式は、ニュートンの運動方程式(運動量保存則)を流体要素に適用し、さらに粘性による内部摩擦力を考慮したものです。非圧縮性流体(密度が一定)の場合、次のように表されます:
$$
\rho \left( \frac{\partial \mathbf{u}}{\partial t} + (\mathbf{u} \cdot \nabla) \mathbf{u} \right) = -\nabla P + \mu \nabla^2 \mathbf{u} + \mathbf{f}
$$
ここで、
- \(\rho\):流体の密度
- \(\mathbf{u}\):速度ベクトル場(各点での流体の速度)
- \(P\):圧力場
- \(\mu\):動粘性係数(粘性係数)
- \(\mathbf{f}\):外力(重力など)
この方程式の各項の意味を技術的に詳しく解説します。
左辺:流体要素の加速度(運動量の変化)
- \(\frac{\partial \mathbf{u}}{\partial t}\)(非定常項):ある位置での速度の時間変化を表します。
- \((\mathbf{u} \cdot \nabla) \mathbf{u}\)(移流項):流体が空間的に異なる速度を持つ領域を移動することで生じる速度変化です。これは「慣性項」とも呼ばれ、非線形性の源です。乱流や渦の発生など、流体の複雑な挙動の主因となります。
右辺:流体に働く力
- \(-\nabla P\)(圧力勾配項):圧力の高い場所から低い場所へ流体を押し出す力です。
- \(\mu \nabla^2 \mathbf{u}\)(粘性項・拡散項):速度場のラプラス演算子((\nabla^2))は、周囲との速度差を均そうとする拡散的な効果を表します。粘性が大きいほど、速度のムラが速やかに消えていきます。数学的には、各成分ごとに2階微分を取ることで、局所的な速度の「滑らかさ」を評価しています。
- \(\mathbf{f}\)(外力項):重力や電磁力など、外部から加わる力をまとめて表します。
数学的背景と導出のポイント
ナビエ・ストークス方程式は、
- 質量保存(連続の式)
- 運動量保存(ニュートンの第2法則)
- 応力テンソルの分解(圧力と粘性応力)
を組み合わせて導出されます。特に粘性応力は、ニュートン流体の場合「速度勾配に比例する」という仮定(ニュートンの粘性法則)に基づき、ラプラス演算子の形で表現されます。
非圧縮性条件(連続の式)
非圧縮性流体では、流体の密度が時間・空間的に一定であることから、体積保存の条件が課されます。これが「連続の式」です:
$$
\nabla \cdot \mathbf{u} = 0
$$
この式は「任意の体積要素において、流入する流体の量と流出する量が常に等しい」ことを意味します。ナビエ・ストークス方程式と連続の式を同時に満たす速度場・圧力場を求めることが、非圧縮性流体の運動を記述する本質となります。
工学・物理学的意義
ナビエ・ストークス方程式は、配管流れ、航空機の空力設計、気象・海洋現象、血流や微小流体デバイスなど、極めて広範な分野で応用されています。特に「移流項」と「粘性項」のバランスが、層流・乱流の遷移や流れの安定性を決定づけます。
3. 粘性項の役割:流れを「滑らかにする」
粘性項 \(\mu \nabla^2 \mathbf{u}\) は、別名「拡散項」とも呼ばれます。これは、熱伝導方程式(拡散方程式)における温度の拡散と数学的に同じ構造を持ち、速度のムラ(勾配)を均一にしようとする働きがあるからです。
この項はラプラス演算子(\(\nabla^2\))を含み、ある点の速度とその周囲の速度との差を評価します。速度場に急激な変化や局所的な乱れがあると、粘性項がそれを周囲に拡散し、全体を滑らかに保とうとします。分子論的には、分子の熱運動や分子間力による運動量の拡散がマクロな粘性効果として現れます。
粘性項は流体の運動エネルギーを熱エネルギーへと変換する「エネルギー散逸」の役割も担います。これにより、流れの中の高周波成分(急激な速度変化やノイズ)は減衰し、数値シミュレーション上ではローパスフィルタのような効果を持ちます。
粘性が強い流体では、局所的な速度の乱れがすぐに周囲に拡散して消えてしまい、流れは安定で滑らか(層流)になります。逆に粘性が極めて低い、または流速が非常に大きい場合(レイノルズ数が大きい場合)、拡散が追いつかず、流れは不安定になり「乱流」へと発展します。
また、粘性項は境界層の形成や流れの安定性にも大きく関与します。例えば、パイプ流れや航空機翼周りの流れ、血管内の血流、気象現象など、工学・自然界の多様な現象で粘性項の効果が現れます。
このように、粘性項は流体の滑らかさ・安定性・エネルギー散逸・現象のスケール選択など、流体力学の本質的な性質を決定づける極めて重要な役割を果たしています。
4. Pythonによる実装:粘性による速度の拡散
NS方程式を一度にすべて解くのはまだ準備が必要ですので、今回はNS方程式のなかで最も重要な「粘性項(拡散項)」のみを抜き出して、Pythonでシミュレーションしてみましょう。
「一部の領域だけ速度が速い」という初期状態から、粘性(摩擦)によって周囲に速度が伝わり、次第に全体が滑らかになっていく様子を視覚化します。
import torch
import matplotlib.pyplot as plt
def solve_viscous_diffusion(u, nu, dx, dy, dt, steps):
"""
粘性による速度の拡散のみを計算する (NS方程式の拡散項)
du/dt = nu * nabla^2 u
Args:
u (torch.Tensor): 初期速度場 (Ny, Nx)
nu (float): 動粘性係数 (mu / rho)
dx, dy (float): 格子間隔
dt (float): タイムステップ
steps (int): 計算ステップ数
"""
u_new = u.clone()
for _ in range(steps):
# ラプラス演算子 (nabla^2 u) の中央差分近似
# 中心点と周囲4点の差をとることで「ムラ」を計算する
laplacian = (
(u[1:-1, 2:] - 2*u[1:-1, 1:-1] + u[1:-1, :-2]) / dx**2 +
(u[2:, 1:-1] - 2*u[1:-1, 1:-1] + u[:-2, 1:-1]) / dy**2
)
# 拡散方程式に基づく速度の更新
# u_next = u_current + dt * (nu * laplacian)
u_new[1:-1, 1:-1] = u[1:-1, 1:-1] + dt * nu * laplacian
u = u_new.clone()
return u
# --- パラメータ設定 ---
nx, ny = 50, 50
lx, ly = 2.0, 2.0
dx, dy = lx / (nx - 1), ly / (ny - 1)
nu = 0.1 # 動粘性係数 (大きめに設定して効果を分かりやすくする)
dt = 0.001 # 安定性のために小さな値を設定
# 座標系の作成
x = torch.linspace(0, lx, nx)
y = torch.linspace(0, ly, ny)
Y, X = torch.meshgrid(y, x, indexing='ij')
# --- 初期状態の定義 ---
# 中央の矩形領域だけ右方向に速度(u=1.0)を持っている状態
u_init = torch.zeros((ny, nx))
u_init[20:30, 20:30] = 1.0
# --- 粘性拡散の計算 ---
# 50ステップ後と500ステップ後の状態を計算
u_50 = solve_viscous_diffusion(u_init.clone(), nu, dx, dy, dt, steps=50)
u_500 = solve_viscous_diffusion(u_init.clone(), nu, dx, dy, dt, steps=500)
# --- 可視化 ---
fig, axes = plt.subplots(1, 3, figsize=(18, 5))
titles = ["Initial (t=0)", "After 50 steps", "After 500 steps"]
fields = [u_init, u_50, u_500]
for ax, field, title in zip(axes, fields, titles):
im = ax.imshow(field.numpy(), extent=[0, lx, 0, ly], origin='lower', cmap='magma', vmin=0, vmax=1)
ax.set_title(title)
ax.set_xlabel("x")
ax.set_ylabel("y")
plt.colorbar(im, ax=axes.ravel().tolist(), label='Velocity u')
plt.show()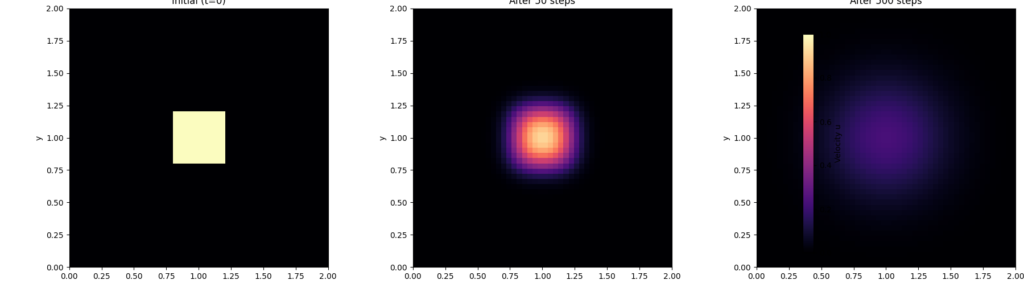
コードの解説
- ラプラス演算子の実装:
laplacianの計算部分に注目してください。ある格子点の値と、その上下左右の格子点の値を比較しています。「自分と周りの平均との差」を計算していることになり、これが拡散のドライビングフォース(原動力)となります。 - 動粘性係数 \(\nu\) (ニュウ):
コード内のnuは、粘性係数 \(\mu\) を密度 \(\rho\) で割った「動粘性係数」です。これが大きいほど、速度のムラが早く解消されます。 - シミュレーション結果:
初期状態ではカクカクしていた速度の分布が、時間が経つにつれて周囲ににじみ出し、丸みを帯びていく様子が見て取れます。これが粘性の本質的な働きです。現実の空気や水の中でも、このようにして運動量が周囲に伝わり、流れが滑らかになっていくのです。
5. ナビエ・ストークス方程式がなぜ「未解決」なのか
余談ですが、このナビエ・ストークス方程式の「滑らかな解が常に存在するかどうか」という問題は、数学のミレニアム懸賞問題のひとつ(100万ドルの懸賞金!)として今も未解決です。
特に「移流項(慣性)」が「粘性項(拡散)」に勝ってしまうとき、流れは非常に小さな渦を無数に含む「乱流」になります。粘性には流れを落ち着かせる効果がありますが、移流には流れをかき乱す効果があります。この2つのせめぎ合いが、流体力学の難しさであり、同時に最大の魅力でもあるのです。
6. まとめと次回の予告
第4回では、現実の流体計算の主役である方程式について学びました。
- 流体の内部摩擦を表す粘性と粘性係数。
- 粘性・圧力・移流のバランスを記述するナビエ・ストークス方程式。
- 体積変化を許さない非圧縮性条件。
- Pythonを用いた粘性拡散(速度の平滑化)のシミュレーション。
今回で、流体を記述する基本的な物理方程式の紹介は一段落です。しかし、これらの方程式を「どうやってコンピュータで解くか」という戦いはまだ始まったばかりです。
次回、第5回では、計算を始めるために不可欠な「境界条件」と、現象の本質を見抜くためのテクニックである「無次元化」について解説します。レイノルズ数という、流体力学で最も有名なパラメータも登場します。
最後まで読んでいただきありがとうございます。



コメント