こんにちは、JS2IIUです。Pythonで攻略する流体力学シミュレーション連載の第5回です。
前回は、流体力学の王様である「ナビエ・ストークス方程式」を学び、流体が持つ「粘性(粘り気)」が流れを滑らかにする様子をPythonで確認しました。しかし、方程式を知っているだけでは、具体的なシミュレーションを完成させることはできません。
例えば、「パイプの中を流れる水」と「翼の周りを流れる空気」では、支配している方程式は同じナビエ・ストークス方程式ですが、現れる現象は全く異なります。この違いを生み出しているのが、今回学ぶ境界条件(Boundary Conditions)です。
また、シミュレーションの「一般性」を高めるために欠かせない無次元化と、流体力学で最も重要な指標であるレイノルズ数についても詳しく解説します。今回もよろしくお願いします。
1. 境界条件:方程式を「特定の現象」に結びつける
ナビエ・ストークス方程式などの流体の支配方程式は、流体という物質が従う「一般的なルール(普遍法則)」を記述しているに過ぎません。実際のシミュレーションや現象解析では、「どこが壁なのか」「どこから流体が入ってくるのか」「どこから出ていくのか」といった計算領域の端(境界)での条件を明確に定める必要があります。これが境界条件(Boundary Condition)です。
境界条件は、物理現象を「特定の状況」に結びつけるために不可欠です。例えば、同じナビエ・ストークス方程式でも、パイプ流れ・翼まわり・開放水面流れなど、境界条件が異なれば現れる現象も全く異なります。境界条件の設定は、現象の再現性・数値計算の安定性・解の一意性に直結する極めて重要な作業です。
境界条件の数学的な与え方には主に2種類あります。
- ディリクレ境界条件 (Dirichlet boundary condition):
境界で物理量の値そのものを直接指定します。例:壁での速度を 0(\(\mathbf{u}=0\))にする、温度を一定値に保つなど。 - ノイマン境界条件 (Neumann boundary condition):
境界で物理量の「勾配(変化率)」を指定します。例:出口で速度の変化をゼロ(\(\frac{\partial \mathbf{u}}{\partial n} = 0\))にする、熱流束を一定にするなど。
これらの組み合わせや特殊な条件(周期境界、対称境界、自由表面など)も現実の問題ではしばしば用いられます。
代表的な流体の境界条件と物理的意味
- 滑りなし条件 (No-slip condition):
粘性流体では、壁に接している流体粒子は壁と同じ速度になります(静止壁なら \(\mathbf{u} = 0\))。この条件により、壁近傍に速度勾配が生じ、境界層が発達します。分子レベルでは、流体分子が壁分子と衝突し、運動量を失うことでこの現象が生じます。 - 滑りあり条件 (Slip condition):
理想流体や特殊な場合には、壁に沿った速度成分がゼロでなくてもよい(摩擦がない)という条件も使われます。 - 流入条件 (Inflow condition):
計算領域の入口で、速度や流量、圧力などを指定します。流入プロファイル(均一、放物線型など)や乱れの有無も現象に大きく影響します。 - 流出条件 (Outflow condition):
計算領域の出口での条件です。多くの場合、出口では流れが十分に発達していると仮定し、速度や圧力の勾配をゼロ(ノイマン条件)とします。出口条件の選び方は数値計算の安定性に大きく影響します。 - 周期境界条件 (Periodic boundary condition):
流れが繰り返し構造を持つ場合、領域の端と端をつなげる条件です。乱流や格子ボルツマン法などでよく使われます。
数値計算における注意点
境界条件の設定は、数値解法の安定性・精度・物理的妥当性に直結します。特に出口条件や複雑な形状の壁条件は、計算の発散や非物理的な解の原因となることが多いため、現象に応じた適切な選択と実装が不可欠です。
このように、境界条件は「方程式を現実の現象に結びつける架け橋」であり、流体シミュレーションの成否を左右する最重要ポイントのひとつです。
2. 無次元化:スケールに惑わされないために
数値シミュレーションや理論解析において、物理量(速度、長さ、時間、圧力など)をそのまま使うのではなく、無次元化(Nondimensionalization)して扱うことは極めて重要です。
無次元化とは、代表的なスケール(長さ \(L\)、速度 \(U\)、時間 \(T\) など)を基準に、すべての物理量を「比率」や「相対値」として表現し直す操作です。これにより、現象の本質的な構造を明らかにし、異なるスケールの現象を統一的に扱うことができます。
無次元化を行う主な理由は次の通りです。
- 計算精度・安定性の向上:非常に大きな値と小さな値が混在すると、丸め誤差や桁落ちによって計算精度が著しく低下します。無次元化により、すべての変数が同程度のオーダー(通常は0〜1程度)に揃い、数値計算が安定します。
- 現象の一般化・縮約:物理量の絶対値に依存せず、「大きさは違うが本質的には同じ現象」を同一の方程式で記述できます。これにより、実験やシミュレーションの結果をスケール変換して他の状況に適用できます。
- 支配的なパラメータの抽出:無次元化によって、現象を特徴づける本質的な無次元数(例:レイノルズ数、プラントル数など)が自然に現れます。
例えば、長さ \(L\)、速度 \(U\) を基準とした場合:
- 無次元の長さ:\(x^* = \frac{x}{L}\)
- 無次元の速度:\(u^* = \frac{u}{U}\)
- 無次元の時間:\(t^* = \frac{t}{L/U}\)
(\(^*\)は無次元量を表す)
この変換をナビエ・ストークス方程式などの流体方程式に適用すると、元々複数あった物理パラメータ(密度、粘性、長さ、速度など)が、たった1つの無次元数(レイノルズ数)に集約されることが多いです。これにより、異なるスケールの現象を「同じ方程式」として扱うことができ、実験やシミュレーションの汎用性が飛躍的に高まります。
また、無次元化は機械学習における「正規化(Normalization)」や「スケーリング」と同じく、入力データのスケールを揃えてモデルの学習や計算を安定させるのと全く同じ目的を持っています。
無次元化の流体方程式への適用例
ナビエ・ストークス方程式を無次元化すると、\(Re = \frac{UL}{\nu}\)(レイノルズ数)という唯一のパラメータが現れ、現象の性質(層流・乱流など)を決定します。これにより、例えば「模型実験」と「実機」の流れを同じReで比較できるなど、スケールの異なる現象の類似性を議論できます。
数値計算上の注意点
無次元化の際は、基準スケールの選び方(代表長さ、代表速度など)が現象の特徴を適切に反映しているか注意が必要です。また、無次元化後の方程式・境界条件・初期条件もすべて無次元量で記述し直す必要があります。
このように、無次元化は流体力学の理論・実験・数値計算のすべてにおいて不可欠な基本技法です。
3. レイノルズ数:流体の性格を決める唯一の数字
ナビエ・ストークス方程式を無次元化すると、興味深いことが起こります。密度 \(\rho\)、粘性 \(\mu\)、速度 \(U\)、長さ \(L\) といったバラバラだったパラメータが、たった1つの数字に集約されるのです。それがレイノルズ数 (Reynolds number, \(Re\)) です。
$$
Re = \frac{\rho U L}{\mu} = \frac{U L}{\nu}
$$
(ここで \(\nu = \mu/\rho\) は動粘性係数です)
このレイノルズ数は、以下の2つの力の比率を表しています。
- 慣性力: 流れ続けようとする力(分子の \(\rho U L\))
- 粘性力: 流れを止めようとする摩擦力(分母の \(\mu\))
レイノルズ数の物理的・数理的意義
レイノルズ数は、流れの性質(層流か乱流か)や現象のスケール類似性を決定づける極めて重要な指標です。例えば、パイプ流れでは \(Re \lesssim 2000\) で層流、\(Re \gtrsim 4000\) で乱流に遷移します(中間領域は遷移流)。
また、レイノルズ数が同じであれば、流体の種類やスケールが異なっても、流れのパターンや力学的挙動が相似になる(力学的相似則)という特徴があります。これにより、模型実験や数値シミュレーションの結果を実機や他のスケールに適用できます。
レイノルズ数による流れの変化
- \(Re\) が小さい場合(粘性支配): 粘性力が支配的で、流れは層が重なるように滑らかに進みます(層流:Laminar flow)。微小流体デバイスや血管内流れなどで典型的です。
- \(Re\) が大きい場合(慣性支配): 慣性力が支配的となり、わずかな乱れが増幅されて複雑な渦や乱流(Turbulent flow)が発生します。航空機や河川、気象現象など大規模な流れで典型的です。
層流と乱流の遷移点(臨界レイノルズ数)は流れの種類や条件によって異なります。
応用例・数値計算での意義
レイノルズ数は、実験・シミュレーション・設計のすべてで不可欠な指標です。例えば、模型実験で実機と同じReを再現すれば、空力特性や圧力分布などを正確に予測できます。数値計算では、Reの値によって必要な格子分解能や時間ステップ、乱流モデルの選択などが大きく変わります。
このように、レイノルズ数は「流体の性格」を一意に決める最重要パラメータであり、無次元化の最大の利点は「異なるスケールの現象をReで統一的に扱える」ことにあります。
4. Pythonによる実践:境界条件の適用とスケール計算
それでは、実際にPythonコードで境界条件をどのようにプログラムに反映させるかを見てみましょう。今回は、2次元の速度場に対して「流入」「壁(滑りなし)」「流出」の条件を設定するコードを作成します。
import torch
import matplotlib.pyplot as plt
def apply_boundary_conditions(u, v):
"""
速度場(u, v)に対して境界条件を適用する
u: x方向速度, v: y方向速度 (Ny, Nx)
"""
# 1. 上下の壁 (Top and Bottom) -> 滑りなし条件 (No-slip)
# 壁の速度を完全にゼロにする
u[0, :] = 0.0 # 下の壁
u[-1, :] = 0.0 # 上の壁
v[0, :] = 0.0
v[-1, :] = 0.0
# 2. 入口 (Left, Inlet) -> 流入条件 (Inflow)
# 一定の速度プロファイル(放物線型など)を与えることも多いが、ここでは一定値
u[1:-1, 0] = 1.0 # 右向きに速度 1.0
v[1:-1, 0] = 0.0
# 3. 出口 (Right, Outlet) -> 流出条件 (Outflow / Neumann)
# 出口での速度勾配をゼロにする (直前のセルの値をコピー)
u[1:-1, -1] = u[1:-1, -2]
v[1:-1, -1] = v[1:-1, -2]
return u, v
# --- レイノルズ数の計算関数 ---
def calculate_reynolds(velocity, length, viscosity, density=1.0):
"""
物理パラメータからレイノルズ数を計算する
"""
return (density * velocity * length) / viscosity
# --- シミュレーション準備 ---
nx, ny = 50, 20
u = torch.zeros((ny, nx))
v = torch.zeros((ny, nx))
# 物理パラメータの設定 (無次元化を意識)
U_ref = 1.0 # 代表速度
L_ref = 1.0 # 代表長さ
mu = 0.01 # 粘性係数
Re = calculate_reynolds(U_ref, L_ref, mu)
print(f"Simulation Reynolds Number: {Re}")
# 境界条件を適用
u, v = apply_boundary_conditions(u, v)
# 可視化
plt.figure(figsize=(10, 4))
plt.imshow(u.numpy(), origin='lower', cmap='Blues', extent=[0, 5, 0, 2])
plt.colorbar(label='u-velocity')
# ベクトル場の表示 (一部の間隔を間引いて表示)
y, x = torch.meshgrid(torch.linspace(0, 2, ny), torch.linspace(0, 5, nx), indexing='ij')
plt.quiver(x[::2, ::4], y[::2, ::4], u[::2, ::4], v[::2, ::4], color='red', scale=10)
plt.title(f"Velocity Field with BCs (Re = {Re:.1f})")
plt.xlabel("x (Flow direction)")
plt.ylabel("y (Channel width)")
plt.show()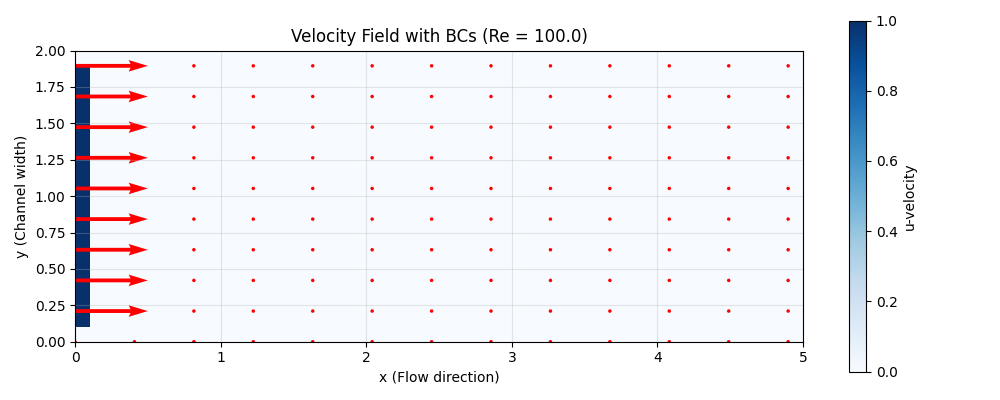
コードの解説
- スライシングによる境界指定:
u[0, :] = 0.0のように、配列の端を指定して値を代入します。これがプログラムにおけるディリクレ境界条件の実装です。 - ノイマン条件(流出)の実装:
u[:, -1] = u[:, -2]という処理は、「一番端のセルの値は、その一つ手前と同じである」ということを意味します。これにより、\(\frac{\partial u}{\partial x} \approx 0\) という勾配ゼロの条件を近似的に実現しています。 - 代表スケールの意識:
コード内ではU_ref = 1.0としています。もし実際の物理現象がU = 10 m/sであっても、無次元化していればプログラム上は1.0として扱い、最後に必要に応じて物理単位に戻せば良いのです。
5. なぜ境界条件で計算が不安定になるのか?
流体計算では、境界付近、特に「出口(流出)」や「複雑な壁形状」の近傍で数値解が急激に変動し、計算が発散・崩壊する現象がしばしば発生します。これは、境界条件の与え方が物理的・数理的に不適切な場合に顕著です。
出口条件の数理的困難
現実の流体は出口の外側にも無限に広がっていますが、数値計算では有限の計算領域で「人工的に切断」せざるを得ません。このとき、出口で与える条件(例:速度や圧力の勾配ゼロ、定常値など)が、実際の流れと矛盾していると、以下のような問題が生じます。
- 反射波・非物理的なノイズ: 出口で発生した数値的なノイズや波が、物理的には外に出ていくはずなのに、計算領域内に「反射」して戻ってきてしまう。
- 情報の遮断・不連続: 出口で流れや圧力の情報が不連続になると、数値的に不安定な解(発散、振動、非物理的な値)が生じやすい。
特に非定常流や乱流では、出口から出ていくべき乱れや渦が領域内に残留・反射し、計算全体が崩壊することもあります。
境界条件の安定化と実装上の工夫
数値シミュレーションで安定かつ物理的に妥当な解を得るためには、以下のような工夫が重要です。
- 非反射境界条件(Non-reflecting/Absorbing BC): 出口で波や乱れが反射せず自然に外へ抜けるような数理的条件(例:Orlanski条件、特性曲線法、スポンジ層の導入など)を用いる。
- 十分に長い計算領域: 出口付近で流れが十分に発達・安定していることを確認し、出口の影響が内部に及ばないようにする。
- 物理現象に即した条件選択: 実験や理論的知見に基づき、現象に最も適した境界条件(速度固定、圧力固定、勾配ゼロなど)を選ぶ。
- 数値スキームとの整合性: 差分法や有限要素法など、用いる数値スキームと境界条件の整合性を保つ(例:高次精度スキームでは境界点の補間や外挿が必要)。
境界条件の選択は「ノウハウ」
境界条件の選択・実装は、単なる「値の指定」ではなく、数値解法の安定性・物理的妥当性・計算効率を左右する高度なノウハウです。特に出口条件は、流体シミュレーションの成否を決める最重要ポイントのひとつです。
このように、適切な境界条件の設計・実装は、方程式を解くアルゴリズムそのものと同じかそれ以上に重要であり、現象理解と数値解析の両面からのアプローチが不可欠です。
6. まとめと次回の予告
第5回では、シミュレーションを「形」にするための重要な作法を学びました。
- 計算領域を定義する境界条件(滑りなし、流入、流出)。
- 現象を一般化し、計算を安定させる無次元化のプロセス。
- 慣性と粘性のバランスを示すレイノルズ数。
- Pythonでの境界条件の具体的な書き方。
ここまでで、流体力学の「物理的な準備」はすべて整いました。いよいよ次回からは、これらの方程式をコンピュータで解くための具体的なテクニック、「差分法」の世界に踏み込みます。
微分という数学的な概念を、どうやってコンピュータが得意な「引き算と割り算」に翻訳するのか。いよいよ数値計算の核心へと迫ります。お楽しみに!
最後まで読んでいただきありがとうございます。



コメント