こんにちはJS2IIUです。Pythonで攻略する流体力学シミュレーション連載の第6回です。
これまで5回にわたり、質量保存則やナビエ・ストークス方程式といった、流体を支配する「物理法則」と「数学的表現」について学んできました。しかし、これらの方程式には大きな問題があります。それは、微分演算子(\(\frac{\partial}{\partial x}\) や \(\nabla\))が含まれていることです。
微分は「無限に小さな変化」を扱う数学的な概念ですが、デジタル計算機であるコンピュータは、無限を直接扱うことができません。コンピュータが得意なのは、有限の数値を使った「足し算、引き算、掛け算、割り算」だけです。
そこで、シミュレーションを実現するためには、連続的な微分方程式を、コンピュータが計算可能な「不連続な(離散的な)式」に翻訳する必要があります。その最も基本的かつ強力な手法が、今回解説する差分法(Finite Difference Method, FDM)です。今回もよろしくお願いします。
1. 差分法とは何か?
差分法(Finite Difference Method, FDM)は、連続的な関数やその微分を、離散的な点の値の差によって近似的に表現・計算する数値解析の基本手法です。特に、微分方程式をコンピュータで解く際に不可欠な技術です。
差分法の背景と意義
現実の物理現象は連続的に変化しますが、コンピュータは有限個の数値しか扱えません。そこで、空間や時間を細かい格子(グリッド)に分割し、各格子点での関数値のみを用いて連続的な微分演算を近似します。これを「離散化」と呼びます。
微分の定義と差分近似
微分の定義は次の通りです:
$$
f'(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) – f(x)}{\Delta x}
$$
しかし、(\Delta x) を無限小にできないため、有限の小さな値を用いて次のように近似します:
$$
f'(x) \approx \frac{f(x + \Delta x) – f(x)}{\Delta x}
$$
このように、微分を「隣り合う点の値の差」で近似するのが差分法の本質です。
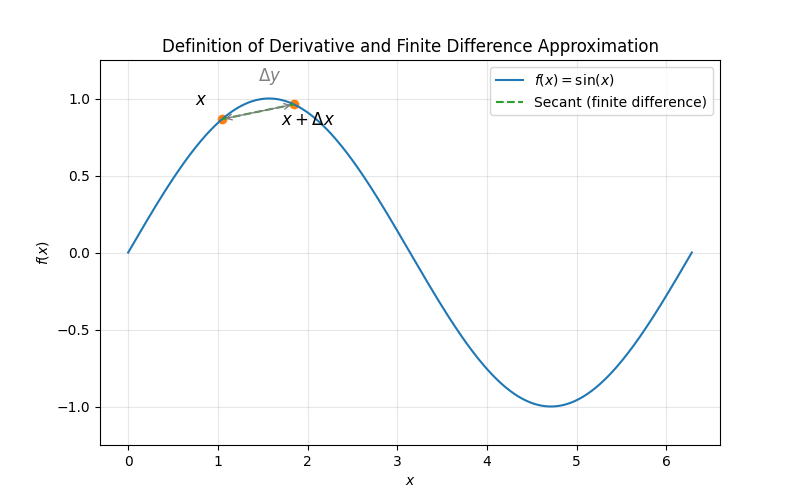
差分近似の種類
差分法では、どの点の値を使うかによっていくつかの近似方法が存在します。
- 前進差分(Forward Difference):\(x\) と \(x+\Delta x\) の値を使う。
- 後退差分(Backward Difference):\(x\) と \(x-\Delta x\) の値を使う。
- 中心差分(Central Difference):\(x-\Delta x\) と \(x+\Delta x\) の値を使い、より高精度な近似が可能。
これらの差分近似は、テイラー展開を用いて導出され、近似誤差(切断誤差)の次数が異なります。中心差分は2次精度、前進・後退差分は1次精度です。
差分法の応用例
差分法は、流体力学・熱伝導・電磁気学など、微分方程式で記述される多くの物理現象の数値シミュレーションに利用されます。例えば、速度場や温度場の勾配、拡散項、移流項などの計算に不可欠です。
離散化のイメージ
例えば、区間 \([a, b]\) を \(N\) 個の等間隔格子点 \(x_0, x_1, …, x_N\) に分割し、格子間隔を \(\Delta x = (b-a)/N\) とします。各格子点での関数値 \(f(x_i)\) を用いて、微分を差分で近似します。
このようにして、連続的な微分方程式を、コンピュータが扱える「差分方程式」に変換することができます。
2. テイラー展開:近似の「正確さ」を保証する魔法の杖
差分法による近似の理論的根拠と精度評価のためには、テイラー展開(Taylor expansion)が不可欠です。テイラー展開は、ある点 \(x\) で十分に滑らかな関数 \(f(x)\) を、その近傍 \(x + \Delta x\) で多項式として近似する方法です。
テイラー展開の一般形
$$
f(x + \Delta x) = f(x) + f'(x)\Delta x + \frac{1}{2!}f”(x)\Delta x^2 + \frac{1}{3!}f”'(x)\Delta x^3 + \cdots
$$
この式は、\(\Delta x\) が十分小さいとき、関数の値を微分係数とその高次導関数で近似できることを示しています。
差分近似とテイラー展開
差分法で使う各種近似式は、テイラー展開の項をどこまで考慮するかによって導かれます。
前進差分 (Forward Difference)
$$
\frac{f(x + \Delta x) – f(x)}{\Delta x} = f'(x) + \frac{1}{2}f”(x)\Delta x + \frac{1}{6}f”'(x)\Delta x^2 + O(\Delta x^3)
$$
この式から、前進差分は1次の誤差(\(O(\Delta x)\))を持つことが分かります。
後退差分 (Backward Difference)
$$
\frac{f(x) – f(x – \Delta x)}{\Delta x} = f'(x) – \frac{1}{2}f”(x)\Delta x + \frac{1}{6}f”'(x)\Delta x^2 + O(\Delta x^3)
$$
これも1次の誤差(\(O(\Delta x)\))です。
中心差分 (Central Difference)
$$
\frac{f(x + \Delta x) – f(x – \Delta x)}{2\Delta x} = f'(x) + \frac{1}{6}f”'(x)\Delta x^2 + O(\Delta x^4)
$$
中心差分では、\(\Delta x\) に比例する誤差項が打ち消し合い、主な誤差は2次(\(O(\Delta x^2)\))となります。これが中心差分が高精度である理由です。
二階微分の差分近似
テイラー展開を2点分使うことで、二階微分も次のように近似できます:
$$
f”(x) \approx \frac{f(x + \Delta x) – 2f(x) + f(x – \Delta x)}{\Delta x^2}
$$
この式も2次精度(\(O(\Delta x^2)\))であり、数値流体力学や拡散方程式の離散化で頻繁に利用されます。
切断誤差(Truncation Error)
テイラー展開を有限項で打ち切ることで生じる誤差を切断誤差と呼びます。差分法の精度は、この切断誤差の次数で評価されます。\(\Delta x\) を小さくするほど誤差は減少しますが、計算コストとのバランスも重要です。
3. Pythonによる実践:近似精度の検証
それでは、Pythonを使って、差分近似が実際にどの程度の精度を持っているかを実験してみましょう。
今回は \(f(x) = \sin(x)\) という関数の微分をターゲットにします。この関数の微分は数学的に \(\cos(x)\) であることが分かっているので、近似値と理論値を比較することで、切断誤差(Truncation error)の挙動を直接観察できます。
import torch
import matplotlib.pyplot as plt
def analytical_derivative(x):
"""理論的な微分値: cos(x)"""
return torch.cos(x)
def forward_difference(f, x, dx):
"""前進差分 (1次精度)"""
return (f(x + dx) - f(x)) / dx
def central_difference(f, x, dx):
"""中心差分 (2次精度)"""
return (f(x + dx) - f(x - dx)) / (2 * dx)
# --- 実験設定 ---
x0 = torch.tensor(1.0) # x = 1.0 における微分を計算
f = torch.sin
true_val = analytical_derivative(x0)
# 格子間隔 (dx) を 1.0 から 10^-4 まで変化させる
dx_list = torch.logspace(0, -4, 20)
error_forward = []
error_central = []
for dx in dx_list:
# 前進差分とその誤差
df_f = forward_difference(f, x0, dx)
error_forward.append(torch.abs(df_f - true_val))
# 中心差分とその誤差
df_c = central_difference(f, x0, dx)
error_central.append(torch.abs(df_c - true_val))
# --- 可視化 ---
plt.figure(figsize=(10, 6))
plt.loglog(dx_list.numpy(), error_forward, 'o-', label='Forward Difference (1st order)')
plt.loglog(dx_list.numpy(), error_central, 's-', label='Central Difference (2nd order)')
# 比較用の勾配線 (O(dx) と O(dx^2))
plt.loglog(dx_list.numpy(), dx_list.numpy() * 0.5, '--', color='gray', label='Slope = 1')
plt.loglog(dx_list.numpy(), dx_list.numpy()**2 * 0.1, '--', color='black', label='Slope = 2')
plt.title("Convergence Study: Grid Spacing vs. Error")
plt.xlabel("Grid Spacing (dx)")
plt.ylabel("Absolute Error")
plt.legend()
plt.grid(True, which="both", ls="-", alpha=0.5)
plt.show()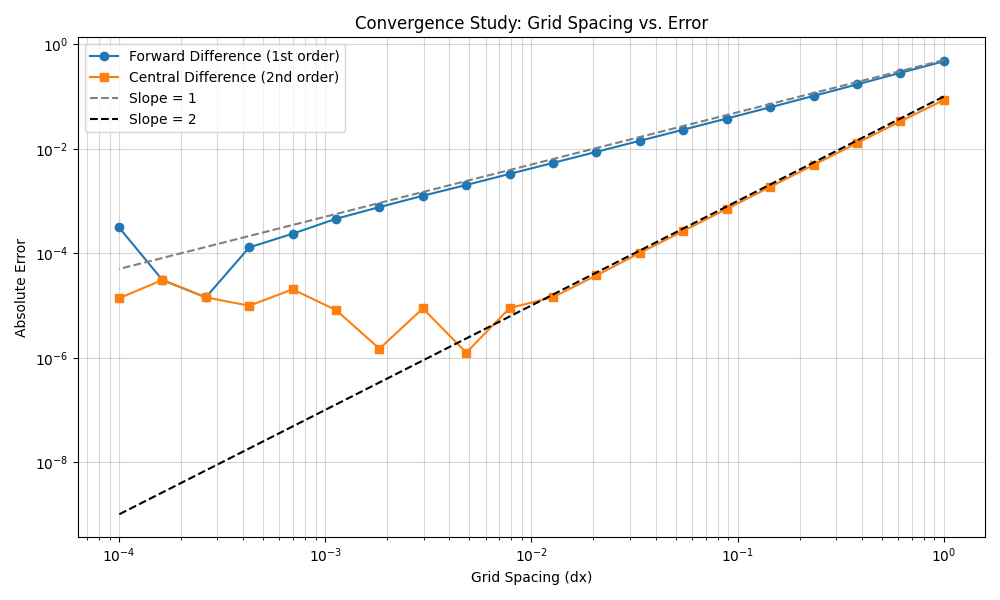
コードの解説
- 対数スケールでのプロット:
誤差の解析にはplt.loglog(両対数グラフ)を使います。なぜなら、誤差が \(O(\Delta x^n)\) のとき、対数グラフ上ではその傾きが精度 \(n\) と一致するからです。 - 傾きの確認:
グラフを見ると、前進差分の誤差はSlope = 1の点線に沿って減少し、中心差分の誤差はSlope = 2の点線に沿って急激に減少していることが分かります。 - 格子間隔 (Grid Spacing) の重要性:
\(\Delta x\) を小さくすればするほど誤差は減りますが、その分だけ計算する格子点の数が増え、メモリや計算時間が必要になります。いかに少ない格子点(大きな \(\Delta x\))で高い精度を得るかが、数値シミュレーションの腕の見せ所です。
4. なぜ常に「中心差分」を使わないのか?
「2次精度の中心差分の方が常に優れているなら、前進や後退差分は不要ではないか?」という疑問を持つ方も多いでしょう。
確かに、数学的な観点からは中心差分は高精度であり、理想的な選択肢に見えます。しかし、実際の流体シミュレーションや数値計算の現場では、必ずしも「精度が高い=最良」とは限りません。
例えば、流れが非常に速い「移流(advection)」の計算では、中心差分を使うと数値的な振動(非物理的なオーバーシュートやアンダーシュート)が発生しやすく、最悪の場合は解が発散してしまうことがあります。これは、中心差分が「安定性(stability)」の面で弱い場合があるためです。
このような場合、あえて精度の低い「上流差分(upwind difference、後退差分の一種)」を使うことで、数値的な振動を抑え、計算を安定させることができます。上流差分は物理的な流れの方向性を反映しやすく、特に移流問題や衝撃波を含む問題で有効です。
このように、数値計算では「精度(Accuracy)」と「安定性(Stability)」のバランスが非常に重要です。どちらか一方だけを追求するのではなく、問題の性質や目的に応じて最適な差分スキームを選択することが、数値流体力学の奥深さであり、実践的な面白さでもあります。
5. まとめと次回の予告
第6回では、コンピュータが物理法則を理解するための翻訳技術を学びました。
- 連続的な微分を離散的な計算に変える差分法。
- 近似の精度を導き出すための土台となるテイラー展開。
- 1次精度の前進・後退差分と、より高精度な2次精度の中心差分。
- Pythonによる切断誤差の検証と、格子間隔の影響。
これで、皆さんはナビエ・ストークス方程式の各項を、プログラムのコードに変換する力を手に入れました。
しかし、正しく翻訳したはずの式を計算させても、時として答えが無限大に発散し、シミュレーションが「爆発」してしまうことがあります。次回、第7回では、計算を最後まで安全に完遂させるための条件、「安定性と精度、LAXの同値定理」について解説します。
最後まで読んでいただきありがとうございます。


コメント