Pythonで攻略する流体力学の数値計算第10回：偏微分方程式の分類と物理的特徴

こんにちはJS2IIUです。Pythonで攻略する流体力学シミュレーション連載の第10回です。

前回、前々回と、私たちは常微分方程式（ODE）の解法について学びました。時間を追って変化を計算する「初期値問題」と、空間全体のバランスを一度に解く「境界値問題」。これらは数値計算の両輪とも言える重要な技術でした。

しかし、流体力学の主役であるナビエ・ストークス方程式は、時間と空間の両方の変化を同時に扱う「偏微分方程式（PDE: Partial Differential Equation）」です。このPDEという巨大な山を攻略するためには、まずその「敵（方程式）」がどのような性質を持っているのかを正しく見極める必要があります。

今回は、偏微分方程式を数学的・物理的特徴に基づいて「楕円型」「放物線型」「双曲型」の3つに分類し、それぞれの型に対してどのような計算戦略を立てるべきかを詳しく解説します。今回もよろしくお願いします。

1. 偏微分方程式の分類：判別式による整理
2. 楕円型偏微分方程式：平衡の世界
3. 放物線型偏微分方程式：拡散の世界
4. 双曲型偏微分方程式：伝播の世界
5. Pythonによる実践：放物線型と双曲型の挙動比較
1. プロット用コード
2. コードの解説と動作結果の物理的意味
6. ナビエ・ストークス方程式への統合
7. まとめと次回の予告

1. 偏微分方程式の分類：判別式による整理

流体力学や物理現象の数値シミュレーションでは、「偏微分方程式（PDE）」が主役となります。しかしPDEと一口に言っても、その性質や解き方は大きく異なります。まず最初に、PDEの「型」を正しく見極めることが、適切な数値計算手法や安定性条件を選ぶうえで極めて重要です。

2変数2階線形PDEの一般形

2つの変数（例えば $x, y$ や $x, t$）に関する2階の線形偏微分方程式は、次のような一般形で表されます：

$$
A\frac{\partial^2 u}{\partial x^2} + B\frac{\partial^2 u}{\partial x \partial y} + C\frac{\partial^2 u}{\partial y^2} + (\text{1階微分以下の項}) = 0
$$

ここで $A, B, C$ は定数（または変数の関数）であり、$u$ は求めたい関数です。

判別式による分類と2次曲線とのアナロジー

この方程式の本質的な性質を決めるのが、係数 $A, B, C$ から構成される「判別式」

$$
D = B^2 – 4AC
$$

です。これは高校数学で学ぶ2次曲線（円・放物線・双曲線）の分類と全く同じ形をしています。

この判別式の値によって、PDEは次の3つの型に分類されます：

楕円型 (Elliptic): $D = B^2 – 4AC < 0$
放物線型 (Parabolic): $D = B^2 – 4AC = 0$
双曲型 (Hyperbolic): $D = B^2 – 4AC > 0$

物理現象との対応

この分類は単なる数学的なラベルではありません。実はそれぞれが、私たちが日常的に目にする物理現象と深く結びついています。

楕円型：領域全体のバランスを瞬時にとる「平衡」現象（例：定常熱伝導、静電場、ポアソン方程式）。
放物線型：ムラをなだらかに均していく「拡散」現象（例：熱伝導方程式、拡散方程式）。
双曲型：情報や波が一定の速度で伝わる「伝播」現象（例：波動方程式、移流方程式）。

このように、判別式による分類は「どんな物理現象を記述しているか」「どんな数値計算手法が適しているか」「どんな安定性条件が必要か」といった実践的な判断の出発点となります。

2. 楕円型偏微分方程式：平衡の世界

楕円型偏微分方程式は、物理現象の中でも「平衡状態」や「定常状態」を記述する際に現れます。ここでは、その代表例や物理的意味、数値計算上の特徴、そして他の型との違いについて詳しく解説します。

代表例と一般形

楕円型PDEの代表例としては、次の2つが挙げられます：

ラプラス方程式（第3回で登場）：

$$
\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0
$$

ポアソン方程式（第9回で登場）：

$$
\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = f(x, y)
$$

これらは、2変数2階線形PDEのうち判別式 $D = B^2 – 4AC < 0$ となるものです。

物理的特徴：平衡と「即時的な影響」

楕円型PDEが記述するのは「時間に依存しない定常状態」です。たとえば、

定常熱伝導（物体の温度分布が時間とともに変化しなくなった状態）
静電場や重力場の分布
流体のポテンシャル流
などが該当します。

最大の特徴は、「領域内のどこか一箇所の条件を変えると、その影響が瞬時に領域全体へ及ぶ」という点です。例えば、定常熱伝導の問題で端の温度を少し変えると、内部の温度分布も全体的に即座に変化し、新しい平衡状態が決まります。これは、情報が無限の速さで伝わるという数学的性質に由来します。

この「全体のバランスを一度に取る」性質は、放物線型（拡散）や双曲型（伝播）とは根本的に異なります。後者では、情報の伝わる速さや伝播範囲に制限がありますが、楕円型ではそのような「遅れ」や「局所性」はありません。

境界値問題としての本質と応用例

楕円型PDEは、境界値問題として現れるのが一般的です。すなわち、領域の端（境界）で値や勾配などの条件を与え、内部の解を一度に決定します。

応用例：

熱伝導の定常分布（物体の端の温度から内部の温度分布を決定）
静電場・重力場の分布（境界の電位や質量分布から場を決定）
流体の定常ポテンシャル流（境界の流速や圧力から流れ全体を決定）

数値計算の戦略：連立一次方程式と反復法

楕円型PDEを数値的に解くには、領域全体を格子点で離散化し、各点の値が周囲の点とバランスを取るような巨大な連立一次方程式を構築します。

この連立方程式を解く方法としては、

ガウス消去法やLU分解などの「行列計算」
ヤコビ法・ガウス＝ザイデル法・SOR法などの「反復法」

が主に使われます。

特に大規模な問題では、反復法によって少しずつ解を修正しながら全体のバランスを取っていく手法が有効です。

3. 放物線型偏微分方程式：拡散の世界

放物線型偏微分方程式は、「拡散」や「平滑化」といった現象を記述する際に現れます。ここでは、その代表例や物理的意味、数値計算上の特徴、そして他の型との違いについて詳しく解説します。

代表例と一般形

放物線型PDEの代表例は、次のような「熱伝導方程式（拡散方程式）」です：

$$
\frac{\partial u}{\partial t} = \alpha \frac{\partial^2 u}{\partial x^2}
$$

ここで $u$ は温度や濃度などの物理量、$\alpha$ は拡散係数です。判別式 $D = B^2 – 4AC = 0$ となる2階線形PDEが放物線型に該当します。

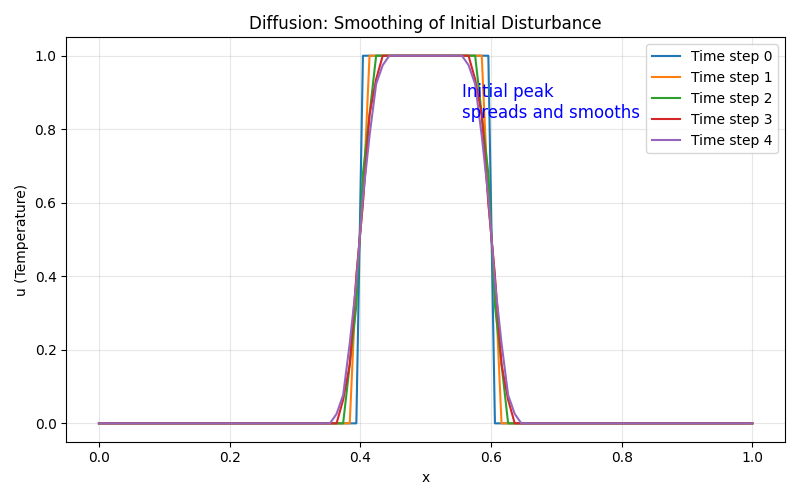
物理的特徴：拡散と平滑化

放物線型PDEが記述するのは、「時間とともに空間的なムラがなまっていく」現象です。たとえば、

熱が物体内をじわじわと伝わっていく（熱伝導）
濃度の高い部分から低い部分へ物質が広がる（拡散）
などが該当します。

この型の最大の特徴は、「情報が有限の速さで未来に向かって伝わる」ことです。楕円型のように全体が即座に影響し合うのではなく、局所的な変化が徐々に周囲へ広がり、やがて全体が滑らかになっていきます。

また、数学的には「無限に遠い場所にも瞬時にわずかな影響が届く」性質も持っていますが、物理的には拡散速度が有限であることが重要です。

流体力学では、第4回で学んだ「粘性（拡散効果）」が放物線型の代表的な例です。粘性によって流体の速度分布がなまっていく様子は、まさに拡散方程式で記述されます。

楕円型・双曲型との違い

放物線型は、

楕円型のような「全体の平衡」ではなく、
双曲型のような「波としての伝播」でもなく、
「局所的なムラが時間とともに滑らかになる」現象を扱います。

この違いは、数値計算のアプローチや安定性条件にも大きく影響します。

数値計算の戦略：時間発展と空間差分

放物線型PDEは、時間発展問題として解きます。すなわち、

現在の状態から、
時間を少し進めて、
新しい状態を計算する

という「逐次的な時間積分」を繰り返します。

このとき、空間方向の2階微分（$\partial^2 u/\partial x^2$）は差分法などで離散化し、時間方向はオイラー法やルンゲ・クッタ法（第8回参照）などの時間積分アルゴリズムを用います。

また、拡散方程式の数値計算では、時間刻み幅や空間刻み幅の選び方によって安定性が大きく左右されるため、安定条件（例：拡散数条件）にも注意が必要です。

4. 双曲型偏微分方程式：伝播の世界

双曲型偏微分方程式は、「波」や「信号の伝播」といった現象を記述する際に現れます。ここでは、その代表例や物理的意味、数値計算上の特徴、そして他の型との違いについて詳しく解説します。

代表例と一般形

双曲型PDEの代表例は、次の2つです：

波動方程式：

$$
\frac{\partial^2 u}{\partial t^2} = c^2 \frac{\partial^2 u}{\partial x^2}
$$

移流方程式：

$$
\frac{\partial u}{\partial t} + a \frac{\partial u}{\partial x} = 0
$$

ここで $c$ は波の伝播速度、$a$ は流体や信号の移動速度です。判別式 $D = B^2 – 4AC > 0$ となる2階線形PDEが双曲型に該当します。

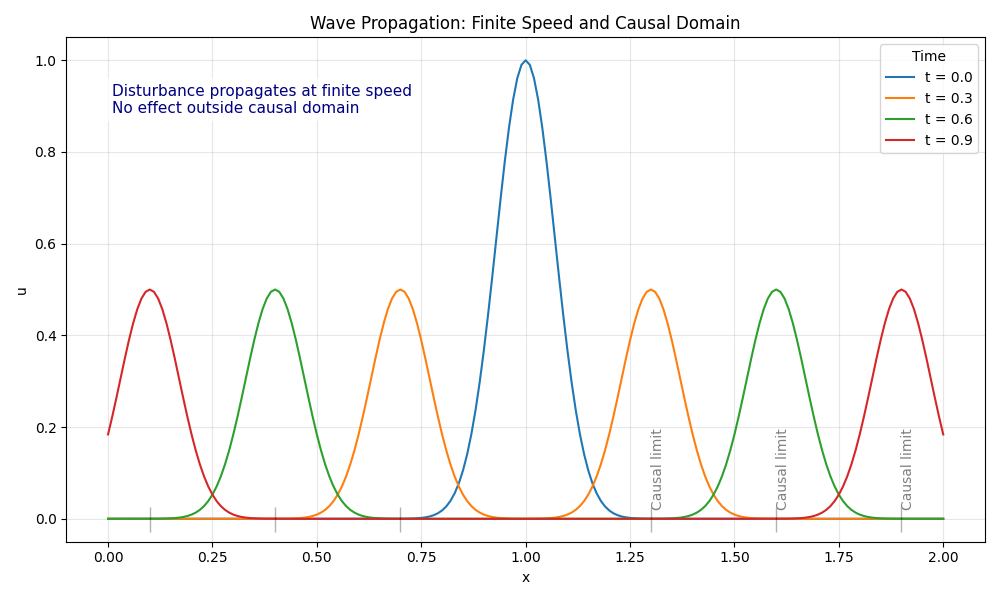
物理的特徴：有限速度での伝播と影響圏

双曲型PDEが記述するのは、「情報や乱れが波として有限の速度で伝わる」現象です。たとえば、

弦や空気中の音波の伝播（波動方程式）
流体や物質の塊が一定速度で運ばれる（移流方程式）
などが該当します。

最大の特徴は、「情報が伝わる範囲（影響圏）が有限で、波が届くまでは遠くの点は何も変化しない」という点です。これは、楕円型（全体が即座に影響し合う）や放物線型（徐々に滑らかになる）とは根本的に異なります。

流体力学では、移流項（慣性項）が双曲型の性質を持ち、波や渦、衝撃波などの現象を記述します。これらは計算上も最も難所となる部分です。

楕円型・放物線型との違い

双曲型は、

楕円型のような「全体の平衡」でもなく、
放物線型のような「拡散・平滑化」でもなく、
「波や信号が有限の速度で伝わる」現象を扱います。

この違いは、数値計算の安定性やアルゴリズム選択に大きく影響します。

数値計算の戦略：CFL条件と安定性

双曲型PDEの数値計算では、CFL条件（Courant–Friedrichs–Lewy条件）が極めて重要です。これは「情報の伝播速度に対して、計算格子の刻み幅と時間刻み幅が適切か」を保証する安定性条件です。

もしCFL条件を満たさないと、数値解が発散したり、物理的にあり得ない振動（数値的振動）が発生したりします。特に移流方程式や波動方程式の計算では、

上流差分法やLax法など、情報の流れを正しく捉える差分法
時間刻み幅の厳密な管理
が不可欠です。

また、双曲型PDEでは「情報の流れる方向（特性線）」を意識した計算が重要となります。これにより、物理的な波の伝播や衝撃波の再現が可能となります。

5. Pythonによる実践：放物線型と双曲型の挙動比較

それでは、PyTorchを用いて「放物線型（拡散）」と「双曲型（移流）」の挙動の違いをシミュレーションしてみましょう。
同じ「矩形波」という初期状態から出発して、時間が経つにつれてどのように形が変わるかを観察します。

Python

import torch
import matplotlib.pyplot as plt

def simulate_pdes(nx=200, nt=100):
    # パラメータ設定
    L = 2.0
    dx = L / (nx - 1)
    dt = 0.005
    x = torch.linspace(0, L, nx)

    # 初期条件: 中央に矩形波を配置
    u_init = torch.zeros(nx)
    u_init[(x >= 0.8) & (x <= 1.2)] = 1.0

    # 放物線型 (拡散) の計算
    # du/dt = nu * d^2u/dx^2
    nu = 0.02 # 拡散係数
    u_para = u_init.clone()

    # 双曲型 (移流) の計算
    # du/dt + a * du/dx = 0
    a = 1.0 # 移流速度
    u_hyper = u_init.clone()

    # 時間発展
    for n in range(nt):
        # 1. 放物線型 (中心差分による拡散)
        d2u_dx2 = (u_para[2:] - 2*u_para[1:-1] + u_para[:-2]) / dx**2
        u_para[1:-1] = u_para[1:-1] + dt * nu * d2u_dx2

        # 2. 双曲型 (上流差分による移流)
        # 安定のために情報の流れてくる方向（左）の点を使う
        du_dx = (u_hyper[1:] - u_hyper[:-1]) / dx
        u_hyper[1:] = u_hyper[1:] - dt * a * du_dx

    return x, u_init, u_para, u_hyper

# 実行
x, u_init, u_para, u_hyper = simulate_pdes()

# 可視化
plt.figure(figsize=(12, 6))
plt.plot(x.numpy(), u_init.numpy(), 'k--', label='Initial (Rectangular Wave)')
plt.plot(x.numpy(), u_para.numpy(), 'r-', label='Parabolic (Diffusion: Smooth)')
plt.plot(x.numpy(), u_hyper.numpy(), 'b-', label='Hyperbolic (Advection: Shift)')

plt.title("Physical Characteristics: Parabolic vs Hyperbolic")
plt.xlabel("x")
plt.ylabel("u")
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()

import torch
import matplotlib.pyplot as plt

def simulate_pdes(nx=200, nt=100):
    # パラメータ設定
    L = 2.0
    dx = L / (nx - 1)
    dt = 0.005
    x = torch.linspace(0, L, nx)

    # 初期条件: 中央に矩形波を配置
    u_init = torch.zeros(nx)
    u_init[(x >= 0.8) & (x <= 1.2)] = 1.0

    # 放物線型 (拡散) の計算
    # du/dt = nu * d^2u/dx^2
    nu = 0.02 # 拡散係数
    u_para = u_init.clone()

    # 双曲型 (移流) の計算
    # du/dt + a * du/dx = 0
    a = 1.0 # 移流速度
    u_hyper = u_init.clone()

    # 時間発展
    for n in range(nt):
        # 1. 放物線型 (中心差分による拡散)
        d2u_dx2 = (u_para[2:] - 2*u_para[1:-1] + u_para[:-2]) / dx**2
        u_para[1:-1] = u_para[1:-1] + dt * nu * d2u_dx2

        # 2. 双曲型 (上流差分による移流)
        # 安定のために情報の流れてくる方向（左）の点を使う
        du_dx = (u_hyper[1:] - u_hyper[:-1]) / dx
        u_hyper[1:] = u_hyper[1:] - dt * a * du_dx

    return x, u_init, u_para, u_hyper

# 実行
x, u_init, u_para, u_hyper = simulate_pdes()

# 可視化
plt.figure(figsize=(12, 6))
plt.plot(x.numpy(), u_init.numpy(), 'k--', label='Initial (Rectangular Wave)')
plt.plot(x.numpy(), u_para.numpy(), 'r-', label='Parabolic (Diffusion: Smooth)')
plt.plot(x.numpy(), u_hyper.numpy(), 'b-', label='Hyperbolic (Advection: Shift)')

plt.title("Physical Characteristics: Parabolic vs Hyperbolic")
plt.xlabel("x")
plt.ylabel("u")
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()

プロット用コード

Python

fig, axes = plt.subplots(3, 1, figsize=(12, 10), sharex=True)

axes[0].plot(x.numpy(), u_init.numpy(), 'k--')
axes[0].set_title("Initial Condition")

axes[1].plot(x.numpy(), u_para.numpy(), 'r-')
axes[1].set_title("Parabolic (Diffusion)")

axes[2].plot(x.numpy(), u_hyper.numpy(), 'b-')
axes[2].set_title("Hyperbolic (Advection)")

for ax in axes:
    ax.grid(True, alpha=0.3)

axes[-1].set_xlabel("x")
plt.tight_layout()
plt.show()

fig, axes = plt.subplots(3, 1, figsize=(12, 10), sharex=True)

axes[0].plot(x.numpy(), u_init.numpy(), 'k--')
axes[0].set_title("Initial Condition")

axes[1].plot(x.numpy(), u_para.numpy(), 'r-')
axes[1].set_title("Parabolic (Diffusion)")

axes[2].plot(x.numpy(), u_hyper.numpy(), 'b-')
axes[2].set_title("Hyperbolic (Advection)")

for ax in axes:
    ax.grid(True, alpha=0.3)

axes[-1].set_xlabel("x")
plt.tight_layout()
plt.show()

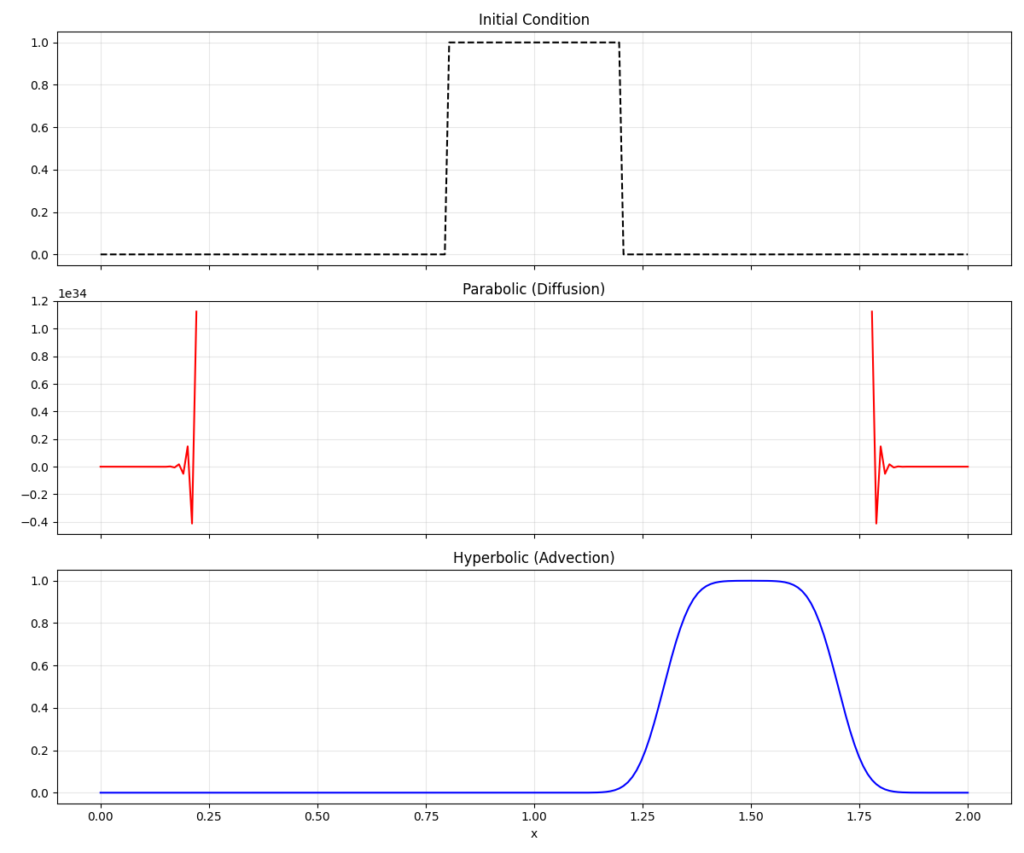
コードの解説と動作結果の物理的意味

放物線型（赤い線）:
初期の鋭い矩形波が、なだらかな山なりに変化しているのがわかります。これが「拡散」の本質です。2階微分の項（拡散項）は、値が高いところを削り、低いところを埋めるように働き、情報を「滑らか」にします。
双曲型（青い線）:
矩形波の形を（多少の数値的ななまりはありますが）保ったまま、右側に「移動」しているのがわかります。これが「伝播（移流）」の本質です。1階微分の項（移流項）は、情報をそのままの形で別の場所へ運びます。
計算上の注意点:
双曲型の計算では、u_hyper[1:] - u_hyper[:-1] という「上流差分」を使っています。これは情報の流れてくる上流側の情報を使うテクニックです。もしここで中心差分を使ってしまうと、第7回で触れた「数値的振動」が発生しやすくなります。

6. ナビエ・ストークス方程式への統合

ここまで「楕円型」「放物線型」「双曲型」という3つのPDEの型とその物理的・数値的特徴を学んできました。いよいよ流体力学の主役であるナビエ・ストークス方程式が、これらすべての性質を内包する「PDEのオールスター」であることが見えてきます。

ナビエ・ストークス方程式の構造と各型の対応

ナビエ・ストークス方程式（非圧縮性の場合）は、次のように書けます：

$$
\frac{\partial \mathbf{u}}{\partial t} + \underbrace{(\mathbf{u} \cdot \nabla) \mathbf{u}}{\text{双曲型（移流）}} = -\frac{1}{\rho}\nabla P + \underbrace{\nu \nabla^2 \mathbf{u}}{\text{放物線型（拡散）}}
$$

$\frac{\partial \mathbf{u}}{\partial t}$：速度場の時間変化
$(\mathbf{u} \cdot \nabla) \mathbf{u}$：双曲型（移流項）…波や乱れが有限速度で伝播
$-\frac{1}{\rho}\nabla P$：圧力勾配項
$\nu \nabla^2 \mathbf{u}$：放物線型（拡散項）…粘性による速度分布の平滑化

さらに、非圧縮性流体では圧力 $P$ を決定するために、次のような楕円型の方程式が現れます：

$$
\nabla^2 P = \dots \quad \underbrace{\text{楕円型（圧力の伝播）}}_{\text{無限速の情報伝達}}
$$

3つの型の同居と数値計算の難しさ

このように、流体シミュレーションでは

双曲型：波や乱れの伝播（移流）
放物線型：粘性による拡散・平滑化
楕円型：圧力による全体バランス
という性質の異なるPDEを、一つのプログラムの中で同時に、かつ矛盾なく扱う必要があります。

それぞれの型は、

伝播速度や影響範囲
数値計算の安定性条件（CFL条件や拡散数条件）
差分法や反復法などの計算手法
が大きく異なります。

例えば、移流項には「上流差分」やCFL条件、拡散項には安定な時間積分法、圧力計算には巨大な連立一次方程式の解法が必要です。

型の「クセ」を理解することの意義

この3つの型の「クセ」を理解していれば、

「なぜこの項にはこの差分法を使うのか？」
「なぜこの計算ステップは爆発しやすいのか？」
「どこにどんな安定性条件が必要なのか？」
といった疑問に対して、明確な根拠を持って数値計算戦略を選択できるようになります。

7. まとめと次回の予告

第10回では、流体計算の攻略図となる偏微分方程式の分類を学びました。

領域全体のバランスを瞬時にとる楕円型（平衡）。
ムラをなだらかに均していく放物線型（拡散）。
情報を一定の速度で運んでいく双曲型（伝播）。
Pythonでのシミュレーションを通じた、拡散と移流の挙動の対比。

今回で、流体力学の基礎理論から数値計算の基礎、そして方程式の分類まで、前半戦の大きな一区切りがつきました。

次回、第11回からは、いよいよ流体計算の「実戦」へと突入します。まずは、移流と拡散が同時に起きる「移流拡散方程式」に挑みます。中心差分で発生する謎の振動問題と、それを解決する「上流差分法」の驚くべきメカニズムについて、詳しく解説していきます。

最後まで読んでいただきありがとうございます。

月	火	水	木	金	土	日
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30	31