こんにちはJS2IIUです。Pythonで攻略する流体力学シミュレーション連載の第12回です。
前回は、物理量が流れに乗って運ばれる「移流」と、周囲に広がる「拡散」が同時に起こる「移流拡散方程式」を扱いました。そこで直面した最大の課題は、中心差分による「数値的振動」と、それを解決するための「上流差分」がもたらす「数値拡散(ボケ)」のトレードオフでした。
これまでの議論では、流速 \(u\) は一定、あるいは外部から与えられる既知の量として扱ってきました。しかし、現実の流体の動きを支配するナビエ・ストークス方程式において、最も厄介で、かつ最も興味深いのは、移流項 \((\mathbf{u} \cdot \nabla)\mathbf{u}\) です。ここでは、「流速自身が、自分自身を運ぶ」という性質を持っています。これが「非線形性」の正体です。
今回は、この非線形移流の「おもちゃ箱」とも言えるバーガース方程式を題材に、流れが急峻になり不連続な壁を作る衝撃波(Shock Wave)の性質と、それを捉えるための高度な数値スキームであるマコーマック法について解説します。今回もよろしくお願いします。
1. 非線形移流:なぜ流体は複雑なのか
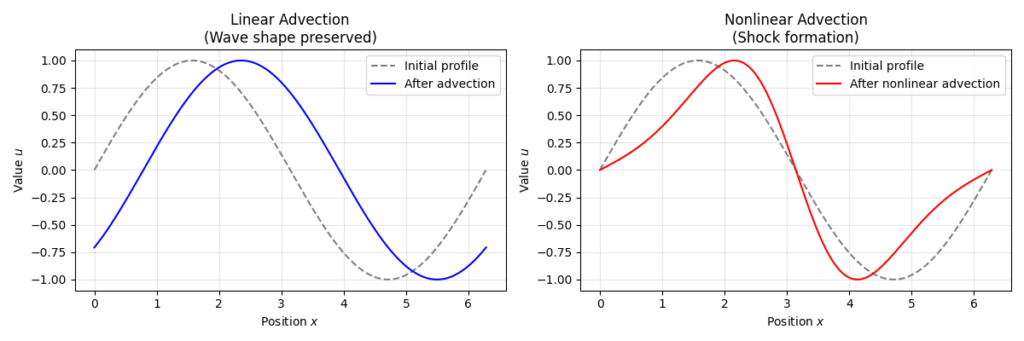
第11回までの「線形移流」では、波の形は保たれたまま一定速度で移動するだけでした。しかし、移流速度が変数 \(u\) 自身に依存する「非線形移流」では、場所によって「情報を運ぶ速さ」が異なります。
もっとも単純な非線形移流の方程式は、以下の形式で書かれます。
非線形移流の最も基本的な数理モデルは、次のような保存則の形で表されます。
$$
\frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} = 0
$$
この式が意味するのは、「大きな値を持つ部分は速く進み、小さな値を持つ部分はゆっくり進む」ということです。これを交通渋滞に例えてみましょう。後ろから非常に速い車(大きな \(u\))がやってきて、前方に遅い車(小さな \(u\))がいる場合、速い車はどんどん前の車に追いついていきます。
物理的な世界では、この「追いつき」が発生すると、波の前面がどんどん急勾配になり、最終的には垂直な壁のような不連続面が形成されます。これが衝撃波の誕生です。
この方程式は、移流速度が場の変数 \(u\) 自身で決まるため、空間的に\(u\)の値が異なる領域では「情報(波形)」の伝播速度も場所ごとに異なります。すなわち、\(u\)が大きい領域ほど速く、小さい領域ほど遅く進むことになります。
この現象を直感的に理解するために、交通流の例を考えてみましょう。\(u\)は車の速度を表すとします。後方から速い車(大きな\(u\))がやってきて、前方に遅い車(小さな\(u\))がいる場合、速い車は次第に前の遅い車に追いつきます。これにより、車列の密度や速度分布に急激な変化が生じ、やがて「渋滞の先頭」のような急峻な勾配が形成されます。
数理的には、波形の高い部分が低い部分を追い越そうとするため、波の前縁が時間とともにどんどん鋭くなり、最終的には理論上「垂直な壁」のような不連続面(勾配が無限大となる点)が現れます。この現象が衝撃波(ショック)の発生です。
非線形移流方程式は、単純な形でありながら、現実の流体や気体の運動における「波の歪み」「衝撃波の形成」といった本質的な非線形現象を捉えることができます。実際の流体力学では、こうした非線形性が複雑な流れやパターンの源となっており、数値計算や理論解析の大きな挑戦となっています。
2. バーガース方程式:ナビエ・ストークスの縮小モデル
ナビエ・ストークス方程式は、現実の流体運動を記述する最も基本的な方程式ですが、そのままでは非常に複雑です。そこで、圧力項を無視し、1次元かつ単一成分の速度場に限定することで、流体力学の本質的な非線形性と拡散の効果を抽出したモデルがバーガース方程式(Burgers’ equation)です。
$$
\frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} = \nu \frac{\partial^2 u}{\partial x^2}
$$
この方程式には、流体現象の2つの根幹的な要素が同居しています。
- 非線形移流項 ((u \frac{\partial u}{\partial x})): これは前節で述べた通り、波形を急峻にし、やがて衝撃波(不連続面)を形成しようとする「非線形性」の源です。大きな(u)を持つ部分が速く進み、波の前縁が鋭くなります。
- 粘性項 ((\nu \frac{\partial^2 u}{\partial x^2})): これは第4回で扱った拡散方程式と同じく、速度場の勾配を滑らかにし、急峻な変化を和らげる働きを持ちます。(\nu)は動粘性係数であり、流体の「拡散しやすさ」を表します。
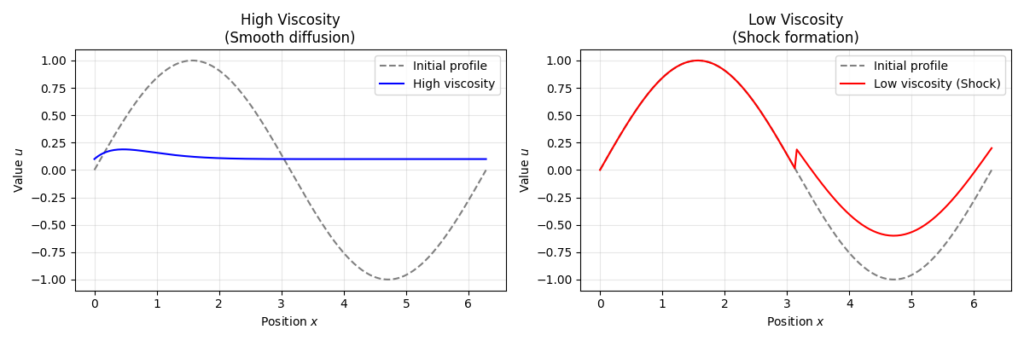
バーガース方程式は、非線形性による波の急峻化と、粘性による平滑化という、相反する2つの物理効果のせめぎ合いを1つの式で表現しています。
特に、粘性 (\nu) が非常に小さい場合、非線形項が支配的となり、波は急激に切り立ってほぼ垂直な不連続面(衝撃波)を形成します。一方、(\nu) が大きい場合は、どんなに急峻な波もすぐに拡散して滑らかになってしまいます。
したがって、衝撃波の「厚み」や波形の鋭さは、この「急峻化しようとする非線形性」と「滑らかにしようとする粘性」のバランスによって決まります。(\nu) が極端に小さい場合、数値計算では衝撃波付近で激しい振動や不安定性が生じやすく、精度よく解くためには高度な数値スキームが必要となります。
3. 数値スキームの精鋭:マコーマック法
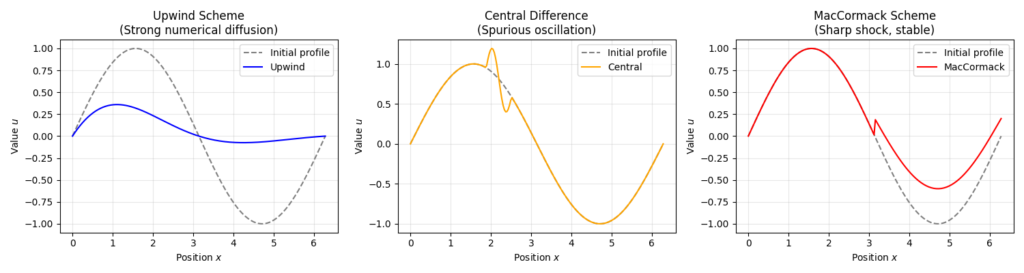
衝撃波のような急激な変化を伴う非線形方程式を数値的に解く際、単純な「上流差分法」では数値拡散が強くなりすぎて波の鋭さが失われてしまいます。一方、中心差分法を用いると、急峻な勾配や不連続面付近で非物理的な振動(ギブス現象)が発生し、計算が破綻しやすくなります。
このような課題を克服するために考案されたのが、マコーマック法(MacCormack method)です。マコーマック法は、計算コストを抑えつつ、時間・空間ともに2次精度を実現し、衝撃波のような急激な変化も比較的高い精度で捉えることができるため、航空宇宙工学や流体力学の分野で広く利用されています。
マコーマック法の特徴は、1ステップの時間発展を「予測」と「修正」の2段階で構成する点にあります。これにより、数値的なバイアスや拡散を抑えつつ、安定性と精度の両立を図っています。
ステップ1:予測ステップ (Predictor)
まず、現時刻の値 (u^n) を用いて、前進差分(空間的に右側の点を参照)で仮の未来値 (\bar{u}) を計算します。
$$
\bar{u}i = u_i^n – \frac{\Delta t}{\Delta x} u_i^n (u{i+1}^n – u_i^n)
$$
この段階では、非線形移流項の差分に前進差分を用いることで、情報が右方向に伝播する効果を強調します。
ステップ2:修正ステップ (Corrector)
次に、予測値\(\bar{u}\) を使い、今度は後退差分(空間的に左側の点を参照)で補正を行い、最終的な新しい値 \(u^{n+1}\) を求めます。
$$
u_i^{n+1} = \frac{1}{2} \left( u_i^n + \bar{u}i – \frac{\Delta t}{\Delta x} \bar{u}_i (\bar{u}_i – \bar{u}{i-1}) \right)
$$
この修正により、前進差分と後退差分の両方の効果をバランスよく取り入れ、中心差分に近い2次精度を実現しつつ、数値的な安定性も確保しています。
このように、マコーマック法は「空間的な揺さぶり」を2段階で与えることで、非線形な勾配や衝撃波のような急激な変化にも強く、かつ過度な数値拡散や振動を抑制できるのが大きな特徴です。
4. 1次元オイラー方程式への展望
バーガース方程式は流速 \(u\) のみを扱う単純なモデルですが、実際の空気やガスのような圧縮性流体では、\(u\) だけでなく「密度(\(\rho\))」「運動量(\(\rho u\))」「全エネルギー(\(E\))」といった複数の保存量が重要となります。これらを同時に扱うのが1次元オイラー方程式です。
$$
\frac{\partial}{\partial t}
\begin{bmatrix} \rho \ \rho u \ E \end{bmatrix}
+ \frac{\partial} {\partial x}
\begin{bmatrix} \rho u \\ \rho u^2 + p \\ (E + p)u \end{bmatrix}
= 0
$$
この保存則の形は、各物理量(質量・運動量・エネルギー)が空間的にどのように移動・変化するかを同時に記述しています。ここで、\(p\) は圧力、\(E\) は単位体積あたりの全エネルギー(内部エネルギー+運動エネルギー)です。
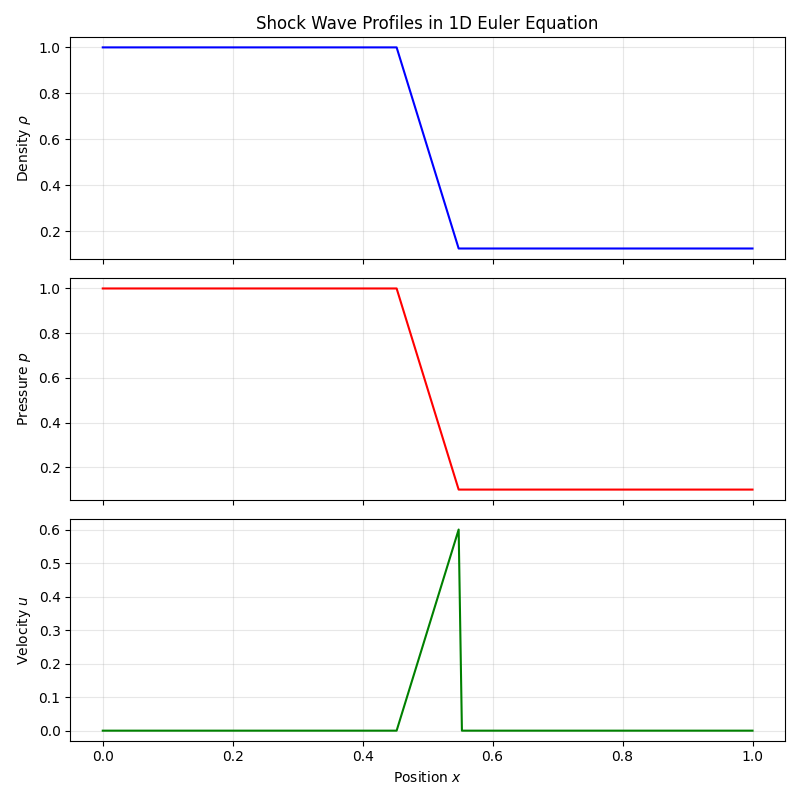
オイラー方程式における衝撃波は、バーガース方程式よりもさらに複雑な現象を示します。具体的には、
- 密度(\(\rho\))の急激な変化
- 圧力(\(p\))の跳ね上がり
- 温度の急上昇
などが同時に発生し、流体の状態が瞬時に大きく変化します。これらは超音速機の衝撃波や爆発現象など、現実の工学・物理分野で極めて重要な現象です。
マコーマック法は、こうした複数の保存則を持つシステムにも適用可能であり、衝撃波を含む圧縮性流体の数値計算においても高い精度と安定性を発揮します。今後は、バーガース方程式で培った知識を基礎に、より複雑なオイラー方程式の世界へと進んでいきます。
5. Pythonによる実装:バーガース方程式の衝撃波シミュレーション
それでは、PyTorchを用いて、バーガース方程式をマコーマック法で解くプログラムを実装してみましょう。粘性が非常に小さい条件で、滑らかなサイン波が次第に切り立った衝撃波へと変化していく様子を観察します。
import torch
import matplotlib.pyplot as plt
def maccormack_burgers(nx=201, nt=150, nu=0.01):
"""
マコーマック法を用いてバーガース方程式を解く
du/dt + u*du/dx = nu*d^2u/dx2
"""
# 領域設定
L = 2.0
dx = L / (nx - 1)
x = torch.linspace(0, L, nx)
# 時間刻み (CFL条件を考慮)
dt = 0.002
# 初期条件: 滑らかなサイン波
# 左側の速い部分が、右側の遅い部分を追い越そうとする
u = torch.sin(2 * torch.pi * x)
# 結果保存用
u_history = [u.clone()]
for n in range(nt):
u_n = u.clone()
# --- 1. 予測ステップ (Predictor: 前進差分) ---
# 移流項は前進差分、拡散項は中心差分
u_star = u_n.clone()
# スライシングによる一括計算
# u_star[i] = u[i] - dt/dx * u[i] * (u[i+1] - u[i]) + dt*nu/dx^2 * (u[i+1] - 2u[i] + u[i-1])
u_star[1:-1] = u_n[1:-1] \
- (dt / dx) * u_n[1:-1] * (u_n[2:] - u_n[1:-1]) \
+ (nu * dt / dx**2) * (u_n[2:] - 2*u_n[1:-1] + u_n[:-2])
# 境界条件 (周期境界)
u_star[0] = u_star[-2]
u_star[-1] = u_star[1]
# --- 2. 修正ステップ (Corrector: 後退差分) ---
# 移流項は後退差分、拡散項は中心差分
u_new = u_n.clone()
u_new[1:-1] = 0.5 * (u_n[1:-1] + u_star[1:-1] \
- (dt / dx) * u_star[1:-1] * (u_star[1:-1] - u_star[:-2]) \
+ (nu * dt / dx**2) * (u_star[2:] - 2*u_star[1:-1] + u_star[:-2]))
# 境界条件 (周期境界)
u_new[0] = u_new[-2]
u_new[-1] = u_new[1]
u = u_new
if n % 30 == 0:
u_history.append(u.clone())
return x, u_history
# --- シミュレーション実行 ---
x, history = maccormack_burgers(nu=0.002) # 粘性を小さくして衝撃波を際立たせる
# 可視化
plt.figure(figsize=(10, 6))
colors = plt.cm.viridis(torch.linspace(0, 1, len(history)))
for i, u_t in enumerate(history):
plt.plot(x.numpy(), u_t.numpy(), color=colors[i], label=f'Step {i*30}')
plt.title("Evolution of Burgers' Equation (MacCormack Method)")
plt.xlabel("Position (x)")
plt.ylabel("Velocity (u)")
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()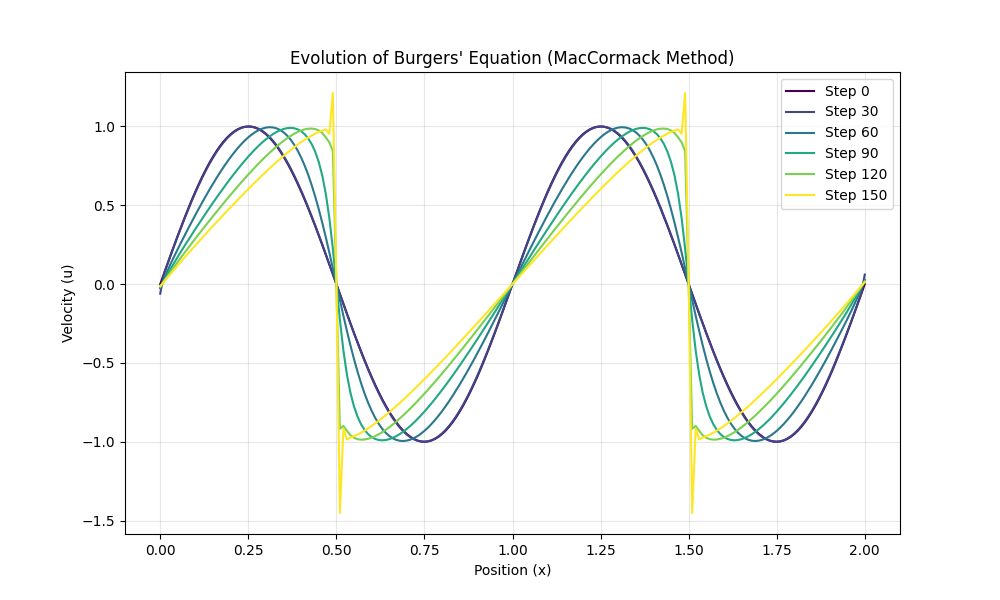
コードの解説と動作のポイント
- 予測と修正のスイッチ:
u_starの計算(予測)では(u_n[2:] - u_n[1:-1])(右側の点を使用)、u_newの計算(修正)では(u_star[1:-1] - u_star[:-2])(左側の点を使用)となっている点に注目してください。この「空間的な揺さぶり」が、数値的な偏りを打ち消し、2次精度を実現しています。 - 粘性係数 \(\nu\) の役割:
nu=0.002という小さな値を設定しています。この値が大きすぎると波はすぐに潰れて単なる山になり、小さすぎるとマコーマック法をもってしても衝撃波付近で小さな振動(ギブス現象に近いもの)が発生します。 - スライシングの威力:
PyTorchのテンソル演算u[2:] - u[1:-1]を使うことで、数万点の格子であっても一瞬で計算が終わります。これは、後の連載で扱う大規模な2次元・3次元計算における必須のテクニックです。 - 結果の解釈:
グラフを見ると、最初は滑らかなサイン波だったものが、時間が経つにつれて中央部分(\(x=1.0\)付近)で急激に切り立ち、ほぼ垂直な壁を形成していくのがわかります。これが「非線形性が作り出す衝撃波」の視覚的な証拠です。
6. まとめ:非線形の壁を乗り越える
応用例・実践的な意義
バーガース方程式は、流体力学だけでなく、交通流のモデル(車列の渋滞・密度波)、プラズマ物理、地震波伝播、さらには生体内の集団運動など、非線形波動現象の基礎モデルとして幅広く応用されています。オイラー方程式は、超音速機の衝撃波、爆発・爆風の伝播、ロケット噴射、星間ガスのダイナミクスなど、圧縮性流体の現象解析に不可欠です。これらの方程式を数値的に解くことで、現実の工学・自然現象の予測や設計に直結します。
数値計算の注意点
衝撃波や急峻な勾配を含む流体現象を安定して計算するためには、CFL条件(Courant-Friedrichs-Lewy条件)を必ず満たす必要があります。これは「時間刻みΔtが空間刻みΔxと流速uに対して十分小さいこと」を意味し、数値解の安定性の基礎です。また、マコーマック法以外にも、TVD(Total Variation Diminishing)法やWENO(Weighted Essentially Non-Oscillatory)法など、より高精度かつ高安定なスキームが存在します。実際のシミュレーションでは、問題の性質(衝撃波の有無、計算コスト、精度要求)に応じて最適な手法を選択することが重要です。
衝撃波の計算ができるようになると、超音速の流れや爆風の伝播など、一気にシミュレーションの対象が広がります。また、ここまでの知識は、ナビエ・ストークス方程式の「移流項」を正しく、かつ安定に計算するための強固な土台となります。
さて、ここまで長らく「1次元の世界」で基礎を固めてきましたが、いよいよ次回、第13回からは「2次元流れの解法」へと進出します。2次元になると、「圧力」をどう決めるかという新しい、そして最も重要な課題が現れます。まずは古典的かつ強力な「流れ関数-渦度法」から、多次元流体シミュレーションの世界を攻略していきましょう。
最後まで読んでいただきありがとうございます。



コメント