こんにちは、JS2IIUです。
これまでの連載では、基本的な交通シミュレーション環境の構築から始まり、マルチエージェント化、そしてFinite State Machine(FSM)を用いた状態遷移による行動制御までを解説してきました。
前回までの実装で、車は「前の車がいなければ進む」「近づいたら止まる」という基本的な判断ができるようになりました。しかし、シミュレーション画面を眺めていて、どこか「ロボット的」な不自然さを感じなかったでしょうか?
「前の車がいなくなった瞬間に最高速度で急発進する」
「前の車に追いついた瞬間にピタッと急停止する」
現実のドライバーはもっと滑らかに運転しますよね。今回は、この「カクカクした動き」を卒業し、人間のような滑らかな加減速を実現するための技術を紹介します。
テーマは、Intelligent Driver Model (IDM) の実装です。
単純なif文の条件分岐(ロジック)から、数式を用いた物理モデル(物理挙動)へとステップアップすることで、シミュレーションのリアリティは劇的に向上します。今回もよろしくお願いします。
1. はじめに:なぜ「物理モデル」が必要なのか
前回のFSM(有限オートマトン)のアプローチでは、以下のような離散的なロジックで速度を決めていました。
- 状態が
STOPなら速度 = 0 - 状態が
DRIVEなら速度 = Max
これはゲームのNPC(Non-Player Character)の簡易的な制御としては十分ですが、「渋滞が自然発生する様子」や「事故のリスク分析」といった高度な交通シミュレーションを行うには力不足です。現実の交通現象は、ドライバーが周囲の状況を感じ取り、アクセルとブレーキをアナログに調整することで生まれる非線形(Non-linear)な相互作用だからです。
そこで登場するのが 追従モデル(Car-Following Model) です。これは「前走車との関係性(距離や速度差)」を入力として、ドライバーが次にどうアクセル/ブレーキを踏むか(加速度)を出力する数理モデルの総称です。
今回はその中でも、交通工学の分野で標準的に使われ、かつ実装が比較的容易な IDM (Intelligent Driver Model) を採用します。
2. Intelligent Driver Model (IDM) の仕組み
IDMは一見難しそうな数式に見えますが、コンセプトは非常にシンプルです。ドライバーの頭の中にある「2つの相反する欲求」をバランスさせているだけだからです。
- フリー走行項(アクセル): 邪魔な車がいなければ、自分の希望速度(Desired Speed)まで加速したい。
- 相互作用項(ブレーキ): 前の車に近づきすぎたら、安全な距離を保つために減速したい。
IDMの基本式
IDMによって算出される加速度 $\dot{v}$ は以下の式で表されます。
$$ \dot{v} = a \left[ 1 – \left( \frac{v}{v_0} \right)^\delta – \left( \frac{s^*(v, \Delta v)}{s} \right)^2 \right] $$
少し複雑に見えますが、Pythonコードに直すときはパーツごとに分解すれば簡単です。まずはパラメータの意味を理解しましょう。
重要なパラメータ
シミュレーションの挙動を調整するために、以下の変数が重要になります。
- \(v_0\) (希望速度): 道が空いている時にドライバーが出したい目標速度。
- \(T\) (車頭時間 / Time Headway): 前の車と「何秒分の距離」を空けたいか。例えば $T=1.5$ 秒なら、時速100km走行時は約42mの車間を保とうとします。これが性格(慎重派かイケイケ派か)を決めます。
- \(s_0\) (最小車間距離): 渋滞で完全に停止した時でも確保する最低限の隙間(2mなど)。
- \(a\) (最大加速度): フルアクセル時の加速度。
- \(b\) (快適減速度): 通常のブレーキ時の減速度。
このモデルの優れている点は、「遠くでは滑らかに加速し、前の車に近づくと徐々にブレーキを強め、最終的に安全な車間距離で速度を合わせる」という一連の動作を、たった一つの数式で表現できる点にあります。
3. 実装編:IDMをPythonコードに落とし込む
では、実際にPythonで実装してみましょう。
ここでは、科学計算ライブラリの numpy を使用しますが、基本的な演算のみなので標準ライブラリの math でも代用可能です。
IDM加速度計算関数
まず、現在の自分の状態と前の車の状態を受け取り、次の瞬間の「加速度」を返す関数を作成します。
import numpy as np
import matplotlib.pyplot as plt
def calculate_idm_accel(v, v_lead, distance, params):
"""
IDM (Intelligent Driver Model) に基づく加速度を計算する関数
Args:
v (float): 自分の現在の速度 (m/s)
v_lead (float): 前走車の速度 (m/s)
distance (float): 前走車との車間距離 (m) ※バンパー間の純粋な隙間
params (dict): IDMのパラメータ辞書
Returns:
float: 計算された加速度 (m/s^2)
"""
# パラメータの展開(可読性のため)
v0 = params['v0'] # 希望速度
T = params['T'] # 安全車頭時間
s0 = params['s0'] # 停止時最小車間距離
a = params['a'] # 最大加速度
b = params['b'] # 快適減速度
delta = params['delta'] # 加速指数(通常は4)
# 1. フリー走行項: (v / v0)^delta
# 速度が希望速度に近づくほど、加速力は弱まる
free_road_term = (v / v0) ** delta
# 2. 相互作用項(ブレーキ項)の計算
# 相対速度 (自分の速度 - 相手の速度)
# 正の値なら「近づいている」、負の値なら「離れている」
delta_v = v - v_lead
# "希望車間距離" (Desired Gap) s* の計算
# s* = s0 + (v * T) + (v * delta_v) / (2 * sqrt(a * b))
# 第3項が「相手より速い場合にブレーキを強める」ロジックの核心です
s_star = s0 + (v * T) + (v * delta_v) / (2 * np.sqrt(a * b))
# 実際の距離との比率の二乗
interaction_term = (s_star / distance) ** 2
# 最終的な加速度
accel = a * (1.0 - free_road_term - interaction_term)
return accel数値積分(オイラー法)
加速度が求まったら、それを使って速度と位置を更新する必要があります。
物理シミュレーションでは、時間を短い刻み(\(dt\))に区切り、少しずつ状態を進める数値積分(Numerical Integration)を行います。今回は最も基本的で実装が簡単なオイラー法(Euler Method)を使います。
$$ v_{t+1} = v_{t} + a \times dt $$
$$ x_{t+1} = x_{t} + v_{t} \times dt $$
4. 実験と検証:グラフで見る「滑らかな追従」
作成した関数が正しく動作するか、シンプルなシナリオで実験します。
「遅いトラック(リーダー)に、速い乗用車(フォロワー)が追いつく」という状況をシミュレートし、Matplotlibで挙動をグラフ化してみましょう。
実験用コード
# --- パラメータ設定 ---
# 単位はメートル(m)と秒(s)
params = {
'v0': 30.0, # 希望速度: 30m/s (約108km/h)
'T': 1.5, # 車頭時間: 1.5秒空けたい
's0': 2.0, # 最低車間距離: 2m
'a': 1.0, # 加速性能: 1.0 m/s^2
'b': 1.5, # ブレーキ性能: 1.5 m/s^2
'delta': 4.0 # 加速指数
}
# --- シミュレーション初期設定 ---
dt = 0.1 # 時間刻み (0.1秒)
max_time = 60.0 # シミュレーション時間 (秒)
steps = int(max_time / dt)
# 車両1(リーダー):前を走る車
x1 = 200.0 # かなり前方に配置
v1 = 10.0 # 10m/s (36km/h) で等速走行する遅い車
# 車両2(フォロワー):後ろから追い上げる車
x2 = 0.0 # スタート地点
v2 = 25.0 # 25m/s (90km/h) で勢いよく走っている
# 履歴記録用リスト
time_history = []
v2_history = []
dist_history = []
# --- メインループ ---
current_time = 0.0
for step in range(steps):
# 1. 現時点での車間距離を計算 (リーダー位置 - フォロワー位置 - 車両長)
# ここでは車両長さを5mと仮定
car_length = 5.0
distance = x1 - x2 - car_length
# 安全のため、距離がゼロ以下の場合は計算しない(衝突処理は今回は割愛)
if distance <= 0.1:
distance = 0.1
# 2. IDMでフォロワーの加速度を計算
acc = calculate_idm_accel(v2, v1, distance, params)
# 3. オイラー法で状態更新
# 速度の更新
v2 += acc * dt
if v2 < 0: v2 = 0 # バックはしない
# 位置の更新
x2 += v2 * dt
# リーダーは等速直線運動(加速度0と仮定)
x1 += v1 * dt
# 4. 履歴の保存
time_history.append(current_time)
v2_history.append(v2)
dist_history.append(distance)
current_time += dt
# --- グラフ描画 ---
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(10, 8))
# 速度の変化
ax1.plot(time_history, v2_history, label='Follower Speed', color='blue', linewidth=2)
ax1.axhline(y=v1, color='red', linestyle='--', label='Leader Speed (Target)')
ax1.set_title('Speed Profile: Smooth Deceleration', fontsize=14)
ax1.set_ylabel('Speed (m/s)', fontsize=12)
ax1.legend(fontsize=12)
ax1.grid(True, alpha=0.5)
# 車間距離の変化
ax2.plot(time_history, dist_history, label='Gap to Leader', color='green', linewidth=2)
# 理論上の安全車間距離 (均衡状態) = s0 + v1 * T
safe_gap = params['s0'] + v1 * params['T']
ax2.axhline(y=safe_gap, color='orange', linestyle='--', label=f'Desired Gap ({safe_gap}m)')
ax2.set_title('Gap Profile: Converging to Safe Distance', fontsize=14)
ax2.set_xlabel('Time (s)', fontsize=12)
ax2.set_ylabel('Gap (m)', fontsize=12)
ax2.legend(fontsize=12)
ax2.grid(True, alpha=0.5)
plt.tight_layout()
plt.show()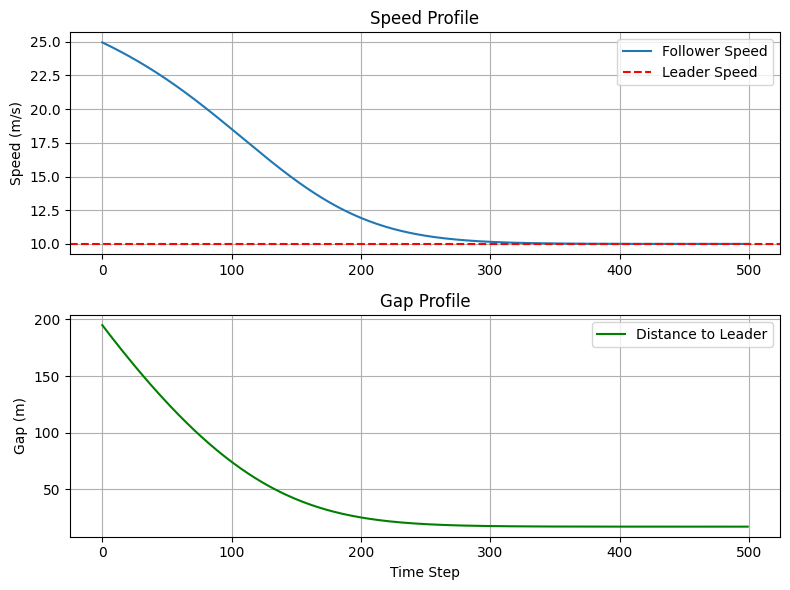
結果の分析
このコードを実行すると、2つのグラフが表示されます。
- Speed Profile (速度変化):
青い線(フォロワー)は、最初は25m/sで走っていますが、赤い破線(リーダーの速度10m/s)に近づくにつれて緩やかに速度を落としていきます。FSMのような「急ブレーキ」ではなく、曲線を描いて収束していく様子が見て取れます。これがIDMの非線形な特性です。 - Gap Profile (車間距離):
緑の線(車間距離)は、最初は急速に縮まりますが、ある一定の距離でピタッと安定します。この安定した距離は、パラメータで設定したT(車頭時間)に基づいた「ドライバーが快適と感じる距離」です。
このように、IDMを使うと「衝突せず、かつ離れすぎず、適切な距離を保って追従する」という高度な制御が、if文を一切書かずに数式だけで実現できるのです。
5. 既存システムへの統合方法
前回の記事で作成した Agent クラスにこの機能を組み込むのは簡単です。update メソッドの中で、固定値で加減速させていた部分を calculate_idm_accel 関数の呼び出しに置き換えるだけです。
class Agent:
def __init__(self, x, v, params):
self.x = x
self.v = v
self.params = params # IDM用パラメータを持たせる
def update(self, dt, leader_agent=None):
if leader_agent:
# 前に車がいる場合:車間距離を計算してIDM
distance = leader_agent.x - self.x - 5.0 # 車両長
acc = calculate_idm_accel(self.v, leader_agent.v, distance, self.params)
else:
# 前に車がいない場合:仮想的に遠くの車がいるか、
# もしくはフリー走行項のみを使って計算
# (distanceを非常に大きくすればフリー走行と同じになります)
acc = calculate_idm_accel(self.v, 0, 10000.0, self.params)
# 状態更新
self.v += acc * dt
if self.v < 0: self.v = 0
self.x += self.v * dtこれにより、すべてのエージェントがIDMに従って自律的に加減速するようになり、列を作って走行する「自然な渋滞」シミュレーションが可能になります。
変更後のサンプルコード全体
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import random
import math
# ==========================================
# 設定パラメータ
# ==========================================
SIMULATION_STEPS = 500 # シミュレーションの総フレーム数
DT = 1.0 # 時間刻み幅 (1ステップを1単位時間とする)
# IDM (Intelligent Driver Model) パラメータ
IDM_PARAMS = {
'v0': 0.6, # 希望速度 (Max Speed)
'T': 5.0, # 安全車間時間 (Time Headway)
'a': 0.05, # 最大加速度
'b': 0.1, # 快適減速度
's0': 2.0, # 最小車間距離 (Jam distance)
'delta': 4.0 # 加速度指数の定数 (通常は4)
}
STOP_LINE = 10.0 # 交差点の中心から停止線までの距離
SPAWN_RATE = 0.08 # 車が発生する確率
CAR_LENGTH = 2.0 # 車両の長さ
# 信号機の設定 (サイクル数)
GREEN_DURATION = 80
YELLOW_DURATION = 20
# ==========================================
# 物理モデル関数 (IDM)
# ==========================================
def calculate_idm_accel(v, v_leader, gap, params):
"""
Intelligent Driver Model (IDM) に基づいて加速度を計算する
v: 自分の速度
v_leader: 前走車の速度
gap: 前走車との車間距離 (純粋な隙間)
params: IDMパラメータ辞書
"""
v0 = params['v0']
T = params['T']
a = params['a']
b = params['b']
s0 = params['s0']
delta = params['delta']
# 接近率 (相対速度: 正なら近づいている)
delta_v = v - v_leader
# IDMの核となる「希望車間距離」の計算
# s* = s0 + v*T + (v * delta_v) / (2 * sqrt(a * b))
s_star = s0 + v * T + (v * delta_v) / (2 * math.sqrt(a * b))
# 加速度の計算
# acc = a * [1 - (v/v0)^delta - (s*/gap)^2]
# gapが非常に小さい(衝突している)場合のゼロ除算防止
if gap <= 0.1:
gap = 0.1
acc = a * (1 - (v / v0)**delta - (s_star / gap)**2)
return acc
# ==========================================
# クラス定義
# ==========================================
class Car:
def __init__(self, x, y, dx, dy, direction, params):
self.x = x
self.y = y
self.dx = dx # 進行方向ベクトル x
self.dy = dy # 進行方向ベクトル y
self.speed = params['v0'] * 0.8 # 初期速度は少し遅めに
self.direction = direction # 'H' (横) or 'V' (縦)
self.params = params
def update(self, cars, traffic_light_state, dt):
# 1. 前方の状況(車および停止線)を確認
min_gap = 10000.0 # 最も近い障害物までの距離
leader_speed = 0.0 # その障害物の速度(停止線なら0)
found_obstacle = False
# --- A. 前走車の探索 ---
for other in cars:
if other is self: continue
# 同じ方向軸かつ同じ向き(対向車でない)を確認
if self.direction == other.direction:
if self.dx * other.dx < 0 or self.dy * other.dy < 0:
continue
dist = 10000.0
# 横方向 (East-West)
if self.direction == 'H':
# 左から右 (dx > 0) かつ 前方にいる
if self.dx > 0 and other.x > self.x:
dist = other.x - self.x - CAR_LENGTH
# 右から左 (dx < 0) かつ 前方にいる
elif self.dx < 0 and other.x < self.x:
dist = self.x - other.x - CAR_LENGTH
# 縦方向 (North-South)
elif self.direction == 'V':
# 下から上 (dy > 0)
if self.dy > 0 and other.y > self.y:
dist = other.y - self.y - CAR_LENGTH
# 上から下 (dy < 0)
elif self.dy < 0 and other.y < self.y:
dist = self.y - other.y - CAR_LENGTH
# 最も近い車を記録
if dist < min_gap:
min_gap = dist
leader_speed = other.speed
found_obstacle = True
# --- B. 信号機(停止線)の探索 ---
dist_to_stop_line = 10000.0
must_stop = False
# 横方向の信号判定 (赤か黄なら停止)
if self.direction == 'H' and traffic_light_state in ['V_GREEN', 'V_YELLOW']:
if self.dx > 0 and self.x < -STOP_LINE: # 左から接近
dist_to_stop_line = -STOP_LINE - self.x
must_stop = True
elif self.dx < 0 and self.x > STOP_LINE: # 右から接近
dist_to_stop_line = self.x - STOP_LINE
must_stop = True
# 縦方向の信号判定
if self.direction == 'V' and traffic_light_state in ['H_GREEN', 'H_YELLOW']:
if self.dy > 0 and self.y < -STOP_LINE: # 下から接近
dist_to_stop_line = -STOP_LINE - self.y
must_stop = True
elif self.dy < 0 and self.y > STOP_LINE: # 上から接近
dist_to_stop_line = self.y - STOP_LINE
must_stop = True
# 信号で止まるべき状況で、停止線の方が前走車より近い場合
# 「速度0の車が停止線にいる」とみなしてIDM計算に使用する
if must_stop and dist_to_stop_line < min_gap:
min_gap = dist_to_stop_line
leader_speed = 0.0 # 停止線は動かない
found_obstacle = True
# 2. 加速度の計算 (IDM)
if found_obstacle:
# 前に車か停止線がある場合
acc = calculate_idm_accel(self.speed, leader_speed, min_gap, self.params)
else:
# フリー走行 (前走車なし = gap無限大、leader_speed=0 として計算)
acc = calculate_idm_accel(self.speed, 0, 10000.0, self.params)
# 3. 速度更新
self.speed += acc * dt
if self.speed < 0: self.speed = 0 # バックはしない
# 4. 位置更新
self.x += self.dx * self.speed * dt
self.y += self.dy * self.speed * dt
class TrafficSimulation:
def __init__(self):
self.cars = []
self.time = 0
self.light_state = 'H_GREEN'
self.light_timer = 0
def step(self):
self.time += 1
self.update_traffic_lights()
self.spawn_cars()
for car in self.cars:
car.update(self.cars, self.light_state, DT)
# 画面外に出た車を削除
self.cars = [c for c in self.cars if -60 < c.x < 60 and -60 < c.y < 60]
def update_traffic_lights(self):
self.light_timer += 1
if self.light_state == 'H_GREEN' and self.light_timer > GREEN_DURATION:
self.light_state = 'H_YELLOW'
self.light_timer = 0
elif self.light_state == 'H_YELLOW' and self.light_timer > YELLOW_DURATION:
self.light_state = 'V_GREEN'
self.light_timer = 0
elif self.light_state == 'V_GREEN' and self.light_timer > GREEN_DURATION:
self.light_state = 'V_YELLOW'
self.light_timer = 0
elif self.light_state == 'V_YELLOW' and self.light_timer > YELLOW_DURATION:
self.light_state = 'H_GREEN'
self.light_timer = 0
def spawn_cars(self):
if random.random() < SPAWN_RATE:
route = random.choice(['W-E', 'E-W', 'S-N', 'N-S'])
# スポーン位置とパラメータ
if route == 'W-E':
spawn_car = Car(-55, -2, 1, 0, 'H', IDM_PARAMS)
elif route == 'E-W':
spawn_car = Car(55, 2, -1, 0, 'H', IDM_PARAMS)
elif route == 'S-N':
spawn_car = Car(-2, -55, 0, 1, 'V', IDM_PARAMS)
elif route == 'N-S':
spawn_car = Car(2, 55, 0, -1, 'V', IDM_PARAMS)
# 出現位置の安全確認
is_safe = True
for c in self.cars:
dist_sq = (c.x - spawn_car.x)**2 + (c.y - spawn_car.y)**2
# IDMパラメータのs0(最小車間)などを考慮して余裕を持たせる
if dist_sq < (IDM_PARAMS['s0'] * 3)**2:
is_safe = False
break
if is_safe:
self.cars.append(spawn_car)
# ==========================================
# 描画
# ==========================================
sim = TrafficSimulation()
fig, ax = plt.subplots(figsize=(6, 6))
def draw_background():
ax.set_xlim(-50, 50)
ax.set_ylim(-50, 50)
ax.set_facecolor('#333333')
# 道路
ax.add_patch(plt.Rectangle((-50, -4), 100, 8, color='#555555'))
ax.add_patch(plt.Rectangle((-4, -50), 8, 100, color='#555555'))
# 白線
ax.plot([-50, 50], [0, 0], color='white', linestyle='--', linewidth=1)
ax.plot([0, 0], [-50, 50], color='white', linestyle='--', linewidth=1)
# 停止線
ax.plot([-4, 4], [-STOP_LINE, -STOP_LINE], color='white', linewidth=2)
ax.plot([-4, 4], [STOP_LINE, STOP_LINE], color='white', linewidth=2)
ax.plot([-STOP_LINE, -STOP_LINE], [-4, 4], color='white', linewidth=2)
ax.plot([STOP_LINE, STOP_LINE], [-4, 4], color='white', linewidth=2)
def init():
return []
def animate(i):
ax.clear()
draw_background()
sim.step()
# 車を描画
for c in sim.cars:
ax.plot(c.x, c.y, 's', color='cyan', markersize=8, markeredgecolor='black')
# 信号表示
light_color_h = 'grey'
light_color_v = 'grey'
if sim.light_state == 'H_GREEN': light_color_h = '#00FF00'; light_color_v = '#FF0000'
elif sim.light_state == 'H_YELLOW': light_color_h = '#FFFF00'; light_color_v = '#FF0000'
elif sim.light_state == 'V_GREEN': light_color_h = '#FF0000'; light_color_v = '#00FF00'
elif sim.light_state == 'V_YELLOW': light_color_h = '#FF0000'; light_color_v = '#FFFF00'
# 信号機インジケータ
ax.text(-45, 42, f"東西: ●", color=light_color_h, fontsize=16, fontweight='bold', path_effects=[])
ax.text(30, 42, f"南北: ●", color=light_color_v, fontsize=16, fontweight='bold', path_effects=[])
ax.set_title(f"Time: {i}")
ax.set_xticks([])
ax.set_yticks([])
return []
ani = animation.FuncAnimation(fig, animate, frames=SIMULATION_STEPS, init_func=init, interval=50)
print("動画生成中...")
try:
ani.save('traffic_simulation_idm.mp4', writer='ffmpeg', fps=20)
print("保存完了: traffic_simulation_idm.mp4")
except:
ani.save('traffic_simulation_idm.gif', writer='pillow', fps=20)
print("保存完了: traffic_simulation_idm.gif")
plt.close()6. まとめ
今回は、交通シミュレーションに「物理的なリアリティ」を与えるための 追従モデル (IDM) の実装について解説しました。
- FSMの限界: 単純なif文制御では、挙動がロボット的で不自然になる。
- IDMの利点: 「希望速度で走りたい」「ぶつかりたくない」という2つの要素を数式化することで、滑らかな追従走行を実現できる。
- 実装のポイント: 加速度を計算し、オイラー法などの数値積分で位置と速度を更新する。
これで、前後の動き(縦方向の制御)に関してはかなり賢いエージェントになりました。
しかし、実際の道路には「隣の車線」があります。前の車が遅ければ、追い越したくなりますよね?
次回は、このIDMに加えて「車線変更モデル(MOBILなど)」を導入し、複数車線での追い越しや割り込みを含めた、さらに複雑な交通流の再現に挑戦します。
最後まで読んでいただきありがとうございました。



コメント