こんにちは、JS2IIUです。
これまでの連載では、物理学に基づいた「社会力モデル」による群衆の動き(第1回)と、コスト関数を用いた「混雑回避の思考」(第2回)を実装してきました。これらによって、エージェントたちは障害物を避け、空いている場所を選ぶことができるようになりました。
しかし、シミュレーションを現実の社会に近づけようとすると、まだ決定的に欠けている行動があります。それは「整列(Queuing)」です。
スーパーマーケットのレジや駅の券売機を想像してください。私たちは前の人にぶつからないように距離を取りつつ、かつ列から離れないようにピタリと後ろにつきます。しかし、従来の「反発力」だけのモデルでこれを再現しようとすると、エージェント同士が互いに反発し合い、列ではなく「団子状の塊」になってしまいます。
今回は、この課題を解決するために、物理演算の世界に「有限オートマトン(FSM)」と「追従行動(Follow-the-Leader)」というアルゴリズムを導入します。カオスな群衆が、規律ある行列を作るまでの技術的なアプローチを解説していきましょう。今回もよろしくお願いします。
はじめに:物理モデルの限界
前回の記事までで実装した「社会力モデル」は、エージェントを「反発し合う粒子」として扱っていました。これは、流体のように人が流れる交差点や通路のシミュレーションには最適です。
しかし、「行列」を作ろうとすると問題が発生します。行列とは「前の人に近づきたい(追従)」と「ぶつかりたくない(反発)」という、矛盾する力が釣り合った状態で維持される構造だからです。単純な物理モデルでは、エージェントは前の人に近づこうとすると弾き飛ばされ、結果として振動したり、列が膨らんだりしてしまいます。
そこで今回は、物理演算のルールを一部上書きし、より上位の「社会的ルール」を組み込みます。
理論編:規律を生む2つのアルゴリズム
整列を実現するために、以下の2つの概念を導入します。
1. 有限オートマトン / ステートマシン (FSM)
エージェントの行動を単一の数式ですべて表現するのは困難です。そこで、エージェントに「状態(State)」を持たせ、状態によって行動ルールを切り替える手法をとります。これを有限オートマトン(Finite State Machine – FSM)と呼びます。
今回は以下の4つの状態を定義します。
- MOVING: 列を探して移動している状態(従来の物理モデル)
- QUEUING: 列に並んでいる状態(追従モード)
- PROCESSING: レジで会計中の状態(停止モード)
- EXITING: 会計が終わり、店を出る状態
2. Follow-the-Leader (追従行動)
「QUEUING」状態のエージェントの目的地は、固定された座標(レジ)ではありません。「自分のひとつ前に並んでいる人」が目的地になります。
これをFollow-the-Leader戦略と呼びます。前の人が進めば自分も進み、止まれば自分も止まる。この連鎖によって行列が形成されます。
実装設計:オブジェクト指向による構造化
これまではゲートを単なる座標として扱っていましたが、行列を管理するためにGateクラスを定義します。
Gateクラス:FIFOキューの管理
待ち行列の基本データ構造はFIFO (First-In-First-Out: 先入れ先出し)です。Pythonのリストを使ってこれを管理します。
class Gate:
def __init__(self, id, pos):
self.id = id
self.pos = pos
# 処理効率係数(0.8なら速い、1.5なら遅い)
self.efficiency = random.uniform(0.8, 1.5)
self.queue = [] # エージェントのリスト (FIFO)
self.current_agent = None # 現在処理中のエージェント
def estimate_wait_time(self):
# 行列の長さ × 処理の遅さ で待ち時間を推定
return len(self.queue) * self.efficiencyこのようにクラス化することで、「このレジは新人さんが担当しているから進みが遅い」といったシミュレーションが可能になります。
実装の壁と解決策
理論通りにコードを書いても、シミュレーションはうまくいきません。ここでは、開発中に直面する典型的な2つの問題とその解決策を紹介します。
課題1:リーダーからの反発(斥力の無効化)
エージェントが前の人(リーダー)の後ろにつこうとすると、前回実装した「他人からの斥力(Social Force)」が働き、後ろに押し返されてしまいます。
解決策:
整列中(QUEUING状態)のエージェントは、「自分が追従している相手」からの斥力を計算から除外(Ignoring Repulsion)」します。
# 斥力計算ループ内での処理イメージ
if other == my_leader:
continue # リーダーからの反発は無視するこれにより、エージェントは前の人にピッタリとくっつくことができるようになります。
課題2:初期配置の矛盾(プリソート)
シミュレーション開始時、エージェントID:0の人が一番後ろにいて、ID:50の人がレジの目の前にいたとします。単純なロジックだと、ID:0の人が「私が先頭だ!」と主張し、ID:50の人がその後ろに並ぼうとして、大逆走が始まります。
解決策:
シミュレーションを開始する前に、エージェントのリストを「レジに近い順(X座標が大きい順)」に並び替えます(プリソート)。
# ゴールに近い順にIDを振り直すイメージ
agents_data.sort(key=lambda p: p[0], reverse=True)これにより、自然な順序で行列形成がスタートします。
完全版コードの実装
それでは、これら全ての要素を統合したPythonコードを紹介します。Agentクラスのupdateメソッド内で、状態に応じた行動分岐(FSM)を行っている点に注目してください。
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from matplotlib.patches import Rectangle
import random
from tqdm import tqdm
import japanize_matplotlib
# --- 設定パラメータ ---
NUM_AGENTS = 100
WIDTH, HEIGHT = 20, 10
GATE_X = 12.0 # レジの位置
GATE_Y_POSITIONS = [2.5, 5.0, 7.5]
SIM_DURATION = 600
DT = 0.1
# FSMの状態定義
STATE_MOVING = 0 # 移動中
STATE_QUEUING = 1 # 整列中
STATE_PROCESSING = 2 # 会計中
STATE_EXITING = 3 # 退出中
class Gate:
def __init__(self, id, y_pos):
self.id = id
self.pos = np.array([GATE_X, y_pos])
# 処理速度のばらつき(小さいほど速い)
self.efficiency = random.uniform(0.8, 1.5)
self.queue = []
self.current_agent = None
def estimate_wait_time(self):
return len(self.queue) * self.efficiency
class Agent:
def __init__(self, id, initial_pos):
self.id = id
self.pos = initial_pos
self.vel = np.array([0.0, 0.0])
self.radius = 0.3
self.max_speed = 1.2 + random.uniform(-0.2, 0.2)
# 必要な処理時間(荷物の量などに相当)
self.required_process_time = random.uniform(1.0, 3.0)
self.remaining_process_time = 0
self.state = STATE_MOVING
self.target_gate = None
self.color = [0, 0, 1] # 青
def select_best_gate(self, gates):
# 最もコスト(待ち時間+距離)が低いゲートを選択
costs = []
for gate in gates:
dist = np.linalg.norm(gate.pos - self.pos)
wait_cost = gate.estimate_wait_time()
total_cost = wait_cost * 2.0 + dist * 0.1
costs.append(total_cost)
return gates[np.argmin(costs)]
def update(self, gates, agents):
# 1. ゲート未決定なら選ぶ
if self.target_gate is None:
self.target_gate = self.select_best_gate(gates)
self.target_gate.queue.append(self)
self.state = STATE_QUEUING
target_pos = None
speed_limit = self.max_speed
my_leader = None # 追従対象
# --- FSM: 状態ごとの振る舞い ---
if self.state == STATE_EXITING:
# 退出:右端へ
target_pos = np.array([WIDTH + 2, self.pos[1]])
self.color = [0.5, 0.5, 0.5] # グレー
elif self.state == STATE_PROCESSING:
# 処理中:停止
self.vel = np.array([0.0, 0.0])
self.color = [1, 0, 0] # 赤
self.remaining_process_time -= DT
if self.remaining_process_time <= 0:
# 処理完了 -> 退出へ遷移
self.state = STATE_EXITING
if self in self.target_gate.queue:
self.target_gate.queue.remove(self)
self.target_gate.current_agent = None
return # 物理演算をスキップして不動にする
elif self.state == STATE_QUEUING:
self.color = [0, 1, 0] # 緑
try:
my_idx = self.target_gate.queue.index(self)
except ValueError:
my_idx = -1
if my_idx == 0:
# 先頭の場合
if self.target_gate.current_agent is None:
# レジが空いていれば進む
target_pos = self.target_gate.pos
# レジ位置に到達したら処理開始
if np.linalg.norm(self.pos - target_pos) < 0.2:
self.state = STATE_PROCESSING
self.target_gate.current_agent = self
# 実際の処理時間 = 荷物量 × レジ係員の遅さ
self.remaining_process_time = self.required_process_time * self.target_gate.efficiency
else:
# 誰か処理中なら待機線で待つ
target_pos = self.target_gate.pos - np.array([1.0, 0])
else:
# 2番目以降:Follow-the-Leader
prev_agent = self.target_gate.queue[my_idx - 1]
my_leader = prev_agent # 斥力除外のために記録
# 前の人の1.0m後ろを目指す
target_pos = prev_agent.pos - np.array([1.0, 0])
# P制御的アプローチ: 近づいたら減速・停止
dist_to_target = np.linalg.norm(self.pos - target_pos)
if dist_to_target < 0.1:
speed_limit = 0.0
elif dist_to_target < 0.5:
speed_limit *= 0.5
# --- 物理力の計算 ---
# 1. 目的地への引力
direction = target_pos - self.pos
dist_target = np.linalg.norm(direction)
if dist_target > 0:
direction /= dist_target
desired_vel = direction * speed_limit
force = (desired_vel - self.vel) / 0.2
# 2. 他人からの斥力(Social Force)
for other in agents:
if other.id != self.id:
# 【重要】リーダーからの斥力は無視する
if other == my_leader:
continue
diff = self.pos - other.pos
dist = np.linalg.norm(diff)
safe_dist = self.radius + other.radius + 0.1
if dist < safe_dist:
# 処理中の人は不動なので強く反発させる
strength = 2000.0 if other.state == STATE_PROCESSING else 500.0
repulsion = strength * np.exp(-(dist / 0.3))
force += (diff / dist) * repulsion
# 3. ノイズ(振動防止のため小さく)
force += np.random.normal(0, 0.1, 2)
# 更新
self.vel += force * DT
speed = np.linalg.norm(self.vel)
if speed > speed_limit:
self.vel = (self.vel / speed) * speed_limit
self.pos += self.vel * DT
# --- メイン処理 ---
gates = [Gate(i, y) for i, y in enumerate(GATE_Y_POSITIONS)]
# 【重要】初期配置のプリソート (Pre-sorting)
# ランダムな位置を生成
temp_agents_data = []
for i in range(NUM_AGENTS):
pos = np.array([random.uniform(0, 8), random.uniform(0, HEIGHT)])
temp_agents_data.append(pos)
# ゴール(右側)に近い順にソートしてIDを割り振る
# これにより「後ろの人が先頭になろうとする」逆走を防ぐ
temp_agents_data.sort(key=lambda p: p[0], reverse=True)
agents = [Agent(i, pos) for i, pos in enumerate(temp_agents_data)]
history = []
print("シミュレーション計算中...")
for t in tqdm(range(SIM_DURATION)):
frame_data = []
frame_colors = []
for agent in agents:
agent.update(gates, agents)
frame_data.append(agent.pos.copy())
frame_colors.append(agent.color)
history.append((frame_data, frame_colors))
# --- 可視化と保存 ---
fig, ax = plt.subplots(figsize=(10, 5))
ax.set_xlim(0, WIDTH)
ax.set_ylim(0, HEIGHT)
ax.set_title("整列行動シミュレーション (FSM + Follow-the-Leader)")
for gate in gates:
rect = Rectangle((gate.pos[0]-0.2, gate.pos[1]-0.4), 0.4, 0.8, color='black')
ax.add_patch(rect)
# 処理効率を表示
ax.text(gate.pos[0], gate.pos[1]+0.5, f"Speed:{gate.efficiency:.1f}", ha='center', fontsize=8)
scat = ax.scatter([], [], c=[], s=60, edgecolor='black')
def animate(i):
positions, colors = history[i]
scat.set_offsets(positions)
scat.set_color(colors)
ax.set_title(f"Time: {i*DT:.1f} s")
return scat,
ani = animation.FuncAnimation(fig, animate, frames=len(history), interval=30, blit=True)
ani.save("simulation_queue.mp4", writer="ffmpeg", fps=30)
print("保存完了")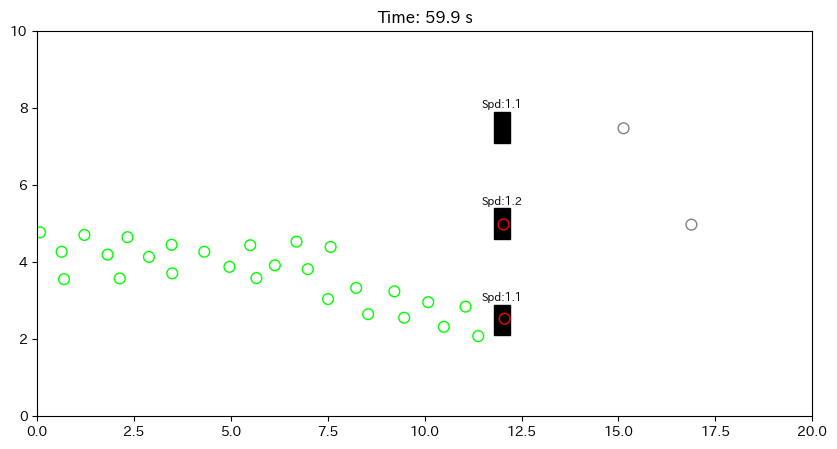
コードの解説
- 状態管理:
Agent.updateメソッド内でself.stateをチェックし、行動ロジックを完全に切り替えています。処理中(赤色)は移動計算自体をスキップし、完全に静止させます。 - リーダー追従:
STATE_QUEUING(緑色)の時、ターゲット座標を固定点ではなくprev_agent.pos(前の人の位置)に基づいて動的に計算しています。 - 斥力の制御:
if other == my_leader: continueの部分が重要です。これがないと、前の人に近づこうとする力と、離れようとする力がケンカして振動してしまいます。
まとめ
本記事では、マルチエージェントシミュレーションに「社会的な規律」を導入しました。
- FSMを用いることで、移動・整列・会計といった複雑な行動遷移を管理しました。
- Follow-the-Leaderと斥力の無効化を組み合わせることで、物理モデルの中にきれいな「行列」を作り出しました。
- プリソートによって、初期状態の矛盾を解消しました。
動画を見ると、処理の遅いレジ(Speed値が大きい)には長い行列ができ、速いレジはサクサク進む様子が確認できるはずです。また、エージェントが会計(赤色)に入ると、後ろの列がピタリと止まり、終わると一斉に動き出す「芋づる式」の動きも再現できています。
これで、私たちのシミュレーションは「ただの点の集まり」から「ルールを持った社会」へと進化しました。このモデルは、レジ配置の最適化や、イベント会場の入場ゲート設計など、実用的な分析に応用可能です。
ぜひパラメータをいじって、「全員の荷物が多い(処理時間が長い)場合」や「レジが故障した場合(効率が極端に悪い)」などを実験してみてください。
最後まで読んでいただきありがとうございました。



コメント